数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装设计
法学统计图中邻居节点之和最多为 K 的节点数量
介绍
无向图是计算机科学和图论中的一个重要组成部分，它表示由边连接的顶点集合，且边没有方向性。与无向图相关的常见问题之一是统计图中邻居节点之和最多为 K 的节点数量。在计算机科学中，图论领域将处理给定矩阵中元素之间的连接。通常，图由边和节点组成。
统计图中节点的数量
在这种情况下，使用的图是无向图。无向图包含 'N' 个节点、'M' 条边，需要满足条件才能获得最多为 K 的节点计数。下面给出一个包含四个节点的无向图的常见示例：
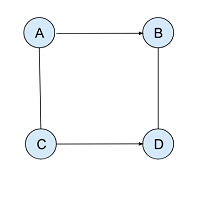
示例
邻接矩阵作为输入，其中包含四个顶点的值。
1 2 2 3 3 4 4 5
邻居是来自节点左侧或右侧的节点。在上述情况下，节点 1 返回邻居之和为 1，节点 2 返回邻居之和为 2，节点 3 返回邻居之和为 3，节点 4 返回邻居之和为 2，最后节点 5 返回邻居之和为 1。我们需要检查节点的和，当邻居之和小于或等于 K 时。因此，节点 1 是唯一满足条件的节点，它返回的值为 1。
方法 1：使用递归函数计算图中邻居节点之和最多为 K 的节点数量的 C 代码
邻接矩阵被初始化为输入，为了遍历列表，我们可以使用深度优先搜索 (DFS) 或广度优先搜索 (BFS) 算法。
算法
步骤 1 − 将所需的标头文件 stdio 和 stdlib 包含在给定的程序中。
步骤 2 − 使用三个参数定义函数：图、N 和 K（int 数据类型）。
步骤 3 − 将计数变量初始化为 0，并使用 for 循环迭代图的邻接列表（从 1 到 N）。
步骤 4 − 边连接两个点 A 和 B，它是给定邻接列表中的相邻节点。
步骤 5 − 将 sum 变量存储在名为“sum”的变量中，该变量对给定顶点中的权重或属性的值求和。
步骤 6 − 检查条件：如果 sum 值小于或等于 K，则将计数加一。
步骤 7 − 最终输出包含图中节点的数量，当邻居节点之和最多为 K 时。
示例
//The header files are included
#include <stdio.h>
#include <stdlib.h>
// Function defined with three arguments and declared as output
int output(int** graph, int node, int edges) {
//Initializing the variable as 0
int val = 0;
//for loop will iterate through the values
for (int m = 1; m <= node; ++m) {
int sum = 0;
for (int neighbor = 1; neighbor <= node; ++neighbor) {
sum += graph[m][neighbor];
}
//To check for the condition whether the sum value is less than or equal to edges
if (sum <= edges) {
//When equal it is incremented by one
val++;
}
}
return val;
}
// Main function to test the code
int main() {
//Initializing the variables with values
int node = 5, M = 4, edges = 2;
int** graph = (int**)malloc((node+1)*sizeof(int*)); // Indexed from 1 to N
for(int i=0; i<=node; ++i){
graph[i] = (int*)malloc((node+1)*sizeof(int));
for(int j=0; j<=node; ++j){
graph[i][j] = 0;
}
}
// The edges values are declared in the graph
graph[1][2] = 1;
graph[2][1] = 1;
graph[2][3] = 1;
graph[3][2] = 1;
graph[3][4] = 1;
graph[4][3] = 1;
graph[4][5] = 1;
graph[5][4] = 1;
//The function is called recursively with the parameters
int nodeCount = output(graph, node, edges);
printf("The total number of nodes with a sum of neighbors less than or equal to %d:\n%d\n", edges, nodeCount);
return 0;
}
输出
The total number of nodes with a sum of neighbors less than or equal to 2: 5
结论
使用 C 程序构建代码——我们可以使用递归函数实现给定无向图的计数。该函数与三个参数一起递归调用。条件是通过 pushback 函数以及通过添加用户给定的值的相邻元素获得的。
172 次浏览
