最多包含 M 个连续节点值为 K 的根到叶路径的数量

---

介绍

二叉树是一种引人入胜的数据结构，在计算机科学和编程中有着广泛的应用。一个有趣的问题是从给定的树中找到从根节点到叶子节点的路径数量，该树由父节点及其子节点组成。二叉树由节点组成，根节点是确定的，并且根据用户的需要可以指定子节点。K 值是确定的，并且 M 值决定了遍历的方式。

根到叶路径的数量

图是用各种节点创建的，这些节点以整数的形式保存值。本文主要关注从起始点或根节点到叶子节点或子节点的路径数量的查找。

示例

图是从二叉树创建的，包含各种节点。

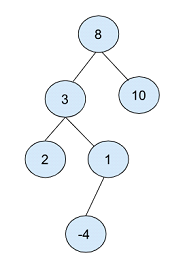
• 在上面的二叉树中，根节点选择为“8”。

• 然后创建两个节点，一个值为 3，另一个值为 10，分别占据根节点的左子节点和右子节点位置。

• 以值为 2 的节点为根节点，再创建两个子节点，值为 2 和 1，分别位于左侧和右侧。

• 最后，值为 1 的子节点创建了一个值为 -4 的子节点。

方法 1：使用递归函数计算最多包含 M 个连续节点值为 K 的根到叶路径的数量的 C++ 代码

为了有效地解决这个问题，我们将利用树遍历算法和递归等基本概念。

算法

步骤 1：创建一个结构来表示树节点，其中包括两个指针（左子节点和右子节点）以及一个用于存储节点值的整数字段。

步骤 2：设计一个递归函数，从二叉树的根节点开始遍历，同时跟踪当前路径长度（初始化为 0）、连续出现次数（最初设置为 0）、目标值 K 和最大允许连续出现次数 M。

步骤 3：根据需要，在每个左子树和右子树上递归调用该函数，传递更新的参数，例如递增的路径长度和连续出现次数。

步骤 4：在遍历过程中，对于每个访问到的非空节点

a) 如果其值等于 K，则将这两个变量都加 1。

b) 如果其值不匹配 K 或已经超过了路径中遇到的 M 个连续出现次数，则将变量重置为零。

步骤 5：在遍历树的过程中，如果子节点在左子节点和右子节点的情况下值都为零，我们可以用两种方式处理：

a) 检查变量是否没有超过 M。

b) 如果是，则将满足条件的从起始到结束的路径总数加 1。

示例

//including the all in one header
#include<bits/stdc++.h>
using namespace std;
//creating structure with two pointers as up and down
struct Vertex {
   int data;
   struct Vertex* up;
   struct Vertex* down;
};
//countPaths function declared with five arguments ; with root = end; Node= vertex; left = up; right = down
int countPaths(Vertex* end, int K, int M, int currCount, int 
consCount) {
//To check the condition when the root is equal to 1 and greater than the maximum value, the values is incremented
   if (end == NULL || consCount > M) {
      return 0;
   }
//To check when the root is equal to the K value, increment by 1
   if (end->data == K) {
      currCount++;
      consCount++;
   } else {
//If it is not equal, it will return 0
      currCount = 0;
   }
   if (end->up == NULL && end->down == NULL) {
      if (currCount <= M) {
         return 1;
      } else {
         return 0;
      }
   }
   return countPaths(end->up, K, M, currCount, consCount) + countPaths(end->down, K, M, currCount, consCount);
}
//Main function to test the implementation
int main() {
   Vertex* end = new Vertex();
   end->data = 8;
   end->up = new Vertex();
   end->up->data = 3;
   end->down = new Vertex();
   end->down->data = 10;
   end->up->up = new Vertex();
   end->up->up->data = 2;
   end->up->down = new Vertex();
   end->up->down->data = 1;
   end->up->down->up = new Vertex();
   end->up->down->up->data = -4;

   int K = 1; // Value of node
   int M = 2; // Maximum consecutive nodes
   int currCount = -1; // Current count
   int consCount = -1; // Consecutive count

   cout << "The number of paths obtained from the given graph of" << M << "nodes with a value of " << K << " is " << countPaths(end, K, M, currCount, consCount) << endl;

   return 0;
} 

输出

The number of paths obtained from the given graph of 2 nodes with a value of 1 is 3

结论

在本文中，我们探讨了计算从顶部（即叶子节点到末端或根节点）开始的路径数量的问题。通过在 C++ 中使用树遍历算法和递归技术，可以有效地解决此类问题。遍历二叉树的过程看起来很困难，但通过示例，它变得很简单。