C++程序：找出图中可减少的最大分数

假设有一个具有n个顶点和m条边的加权无向图。图的分数定义为图中所有边权重的总和。边权重可以为负数，如果移除边，则图的分数增加。我们需要做的就是通过移除边来使图的分数最小化，同时保持图的连通性。我们需要找出可减少的最大分数。

图以数组'edges'的形式给出，其中每个元素的形式为{weight, {vertex1, vertex2}}。

因此，如果输入为n = 5，m = 6，edges = {{2, {1, 2}}, {2, {1, 3}}, {1, {2, 3}}, {3, {2, 4}}, {2, {2, 5}}, {1, {3, 5}}}，则输出为4。

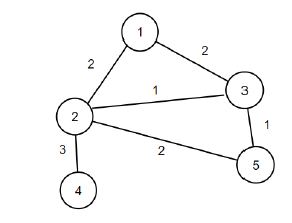
如果我们从图中移除边(1, 2)和(2, 5)，则分数总共减少4，并且图保持连通。

为了解决这个问题，我们将遵循以下步骤：

cnum := 0
Define an array par of size: 100.
Define an array dim of size: 100.
Define a function make(), this will take v,
   par[v] := v
   dim[v] := 1
Define a function find(), this will take v,
   if par[v] is same as v, then:
      return v
   return par[v] = find(par[v])
Define a function unify(), this will take a, b,
a := find(a)
b := find(b)
if a is not equal to b, then:
   (decrease cnum by 1)
   if dim[a] > dim[b], then:
      swap values of (a, b)
   par[a] := b
   dim[b] := dim[b] + dim[a]
cnum := n
sort the array edges based on edge weights
for initialize i := 1, when i <= n, update (increase i by 1), do:
   make(i)
res := 0
for each edge in edges, do:
   a := first vertex of edge
   b := second vertex of edge
   weight := weight of edge
   if find(a) is same as find(b), then:
      if weight >= 0, then:
         res := res + 1 * weight
      Ignore following part, skip to the next iteration
   if cnum is same as 1, then:
      if weight >= 0, then:
         res := res + 1 * weight
   Otherwise
      unify(a, b)
return res

示例

让我们看看下面的实现来更好地理解：

#include <bits/stdc++.h>
using namespace std;

int cnum = 0;
int par[100];
int dim[100];

void make(int v){
   par[v] = v;
   dim[v] = 1;
}
int find(int v){
   if(par[v] == v)
   return v;
   return par[v] = find(par[v]);
}
void unify(int a, int b){
   a = find(a); b = find(b);
   if(a != b){
      cnum--; if(dim[a] > dim[b]){
         swap(a, b);
      }
      par[a] = b; dim[b] += dim[a];
   }
}
int solve(int n, int m, vector <pair <int, pair<int,int>>> edges){
   cnum = n;
   sort(edges.begin(), edges.end());
   for(int i = 1; i <= n; i++)
      make(i);
   int res = 0;
   for(auto &edge : edges){
      int a = edge.second.first;
      int b = edge.second.second;
      int weight = edge.first;
      if(find(a) == find(b)) {
         if(weight >= 0) 
            res += 1 * weight;
         continue;
      }
      if(cnum == 1){
         if(weight >= 0)
            res += 1 * weight;
      } else{
         unify(a, b);
      }
   }
   return res;
}
int main() {
   int n = 5, m = 6;
   vector <pair<int, pair<int,int>>> edges = {{2, {1, 2}}, {2, {1, 3}}, {1, {2, 3}}, {3, {2, 4}}, {2, {2, 5}}, {1, {3, 5}}};
   cout<< solve(n, m, edges);
   return 0;
}

输入

5, 6, {{2, {1, 2}}, {2, {1, 3}}, {1, {2, 3}}, {3, {2, 4}}, {2, {2, 5}}, {1, {3, 5}}}

输出

4

Arnab Chakraborty

更新于：2022年3月2日

250 次浏览

开启你的职业生涯

完成课程获得认证

开始学习