回溯法和分支限界法的区别

---

回溯法是一种用于解决决策问题的算法，而分支限界法是一种用于解决优化问题的算法。这两种技术都遵循蛮力法，并用于生成状态空间树。状态空间树是表示问题所有可能状态的树，从根节点到终端节点。

让我们逐一学习这两种技术，并详细了解它们的区别。

回溯法

回溯法是对蛮力法的改进过程，该技术有效地搜索所有可用选项中的问题解决方案。

蛮力法只不过是找到所有可能的解决方案来满足给定问题。

蛮力法的例子：

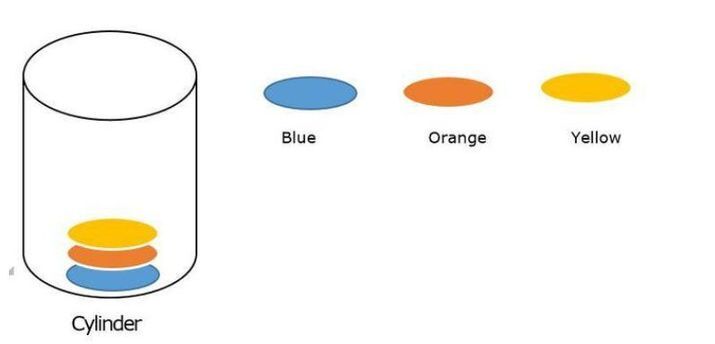
在下图中，有三种颜色需要使用蛮力法的所有可能解决方案填充到圆柱体中。

以下是用颜色填充圆柱体的方法：

• 蓝色、橙色、黄色

• 蓝色、黄色、橙色

• 橙色、蓝色、黄色

• 橙色、黄色、蓝色

• 黄色、蓝色、橙色

• 黄色、橙色、蓝色

共有6种方法可以将颜色填充到圆柱体中，这就是我们可以在回溯法中修改解决方案的方法。

与回溯法相关的以下要点：

• 回溯解决方案可以用树的形式表示，也称为状态空间树。

• 回溯法遵循深度优先搜索 (DFS)。

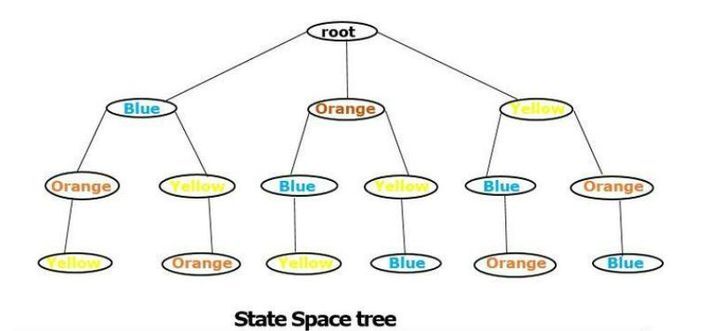
在下图中，我们使用回溯法进行了树形解决方案。

• 根据约束条件，我们根据约束条件解决问题。例如，我们删除每个节点末尾的橙色，这显示了问题时间复杂度的降低。

• 它涉及一个可行性问题。

分支限界法

分支限界法是一种用于解决优化问题的算法，它通过将问题分解成更小的子问题，并通过边界函数消除不包含最优解的子问题来解决。

分支限界搜索是一种将深度优先搜索的节省空间的方法与启发式信息相结合的方法。分支限界搜索的思想是保持最低成本路径或最小路径。

此技术包含两部分：

• 分支 - 找到多个选择

• 限界 - 设置解决方案质量的界限。

分支限界法遵循广度优先搜索 (BFS)。

现在我们使用 BFS 查找 R 到 G 的路线并创建树。

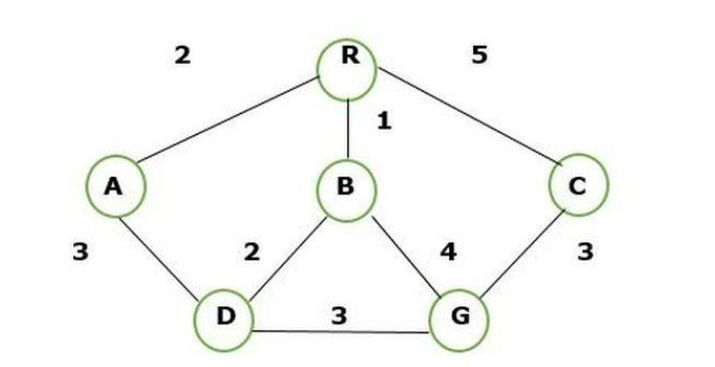
下面给出解决 BFS 方法的步骤：

步骤 1 - 我们知道源节点或根节点是 R。

步骤 2 - 访问根节点的后继节点，即 A、B 和 C。

步骤 3 - 将 A 的路径节点扩展到 D，B 扩展到 D 和 B 扩展到 G，以及 C 扩展到 G。

步骤 4 - 现在完整的结构变为

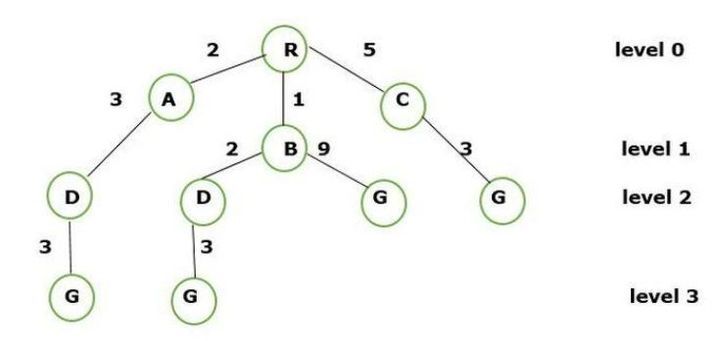
树结构节点的层次空间划分：

层级 0 - R

层级 1 - R -> A，R -> B，R -> C

层级 2 - R -> A -> D，R -> B -> D 和 R -> B -> G，R -> C -> G

层级 3 - 最后，连接路径和节点权重的计算如下所示

R -> A -> D -> G (3+3+2 = 8)，R -> B -> D -> G (3+2+1 = 6) 和 R -> B -> G (9+1 = 10)，R -> C -> G (5+3 = 8)

我们从节点 R 到 G 的最短路径是

R -> B -> D -> G = (3+2+1) = 6

就这样我们解决了广度优先搜索的方法。

与分支限界法相关的以下要点：

• 此技术可以以任何方式遍历 DFS 或 BFS。

• 它涉及一个边界函数。

• 它通过针对最优解来完全搜索状态空间树。

回溯法与分支限界法的区别

参数	回溯法	分支限界法
用途	用于解决基于决策的问题。	用于解决优化问题。
节点	这是一个状态空间树，其中节点探索深度优先搜索。	这探索了优化问题。
效率	更高效。	效率较低。
函数	它涉及可行性函数。	它涉及边界函数。
遍历	它通过深度优先搜索遍历树	它通过广度优先搜索遍历树
解决的问题	回溯法可以解决国际象棋和数独游戏。	它不解决任何游戏问题。
应用	此应用程序用于解决 N 皇后问题、哈密顿循环和基于图着色的问题。	此类应用程序用于解决基于旅行商问题的难题。

结论

我们看到了两种算法之间的区别，更好的方法是分支限界法，它遵循 BFS 搜索。其次，分支限界法的最佳之处在于它针对最优解，而回溯法中的目标节点基于决策问题。在解决这些问题陈述时，BFS 比 DFS 需要更多的内存。