
- 分布式数据库管理系统教程
- DDBMS - 首页
- DDBMS - 数据库管理系统概念
- DDBMS - 分布式数据库
- 分布式数据库设计
- 分布式数据库环境
- DDBMS - 设计策略
- DDBMS - 分布式透明性
- DDBMS - 数据库控制
- 分布式数据库管理系统安全性
- 数据库安全与加密
- 分布式数据库中的安全性
- 分布式数据库管理系统资源
- DDBMS - 快速指南
- DDBMS - 有用资源
- DDBMS - 讨论
关系代数在查询优化中的应用
当提交一个查询时,首先会扫描、解析和验证它。然后创建一个查询的内部表示,例如查询树或查询图。接下来,会设计出从数据库表中检索结果的备选执行策略。选择最合适的查询处理执行策略的过程称为查询优化。
DDBMS 中的查询优化问题
在 DDBMS 中,查询优化是一项至关重要的任务。由于以下因素,其复杂性很高,因为备选策略的数量可能会呈指数级增长:
- 存在多个碎片。
- 碎片或表分布在不同的站点。
- 通信链路的速率。
- 本地处理能力的差异。
因此,在分布式系统中,目标通常是找到一个好的查询处理执行策略,而不是最好的策略。执行查询的时间是以下时间的总和:
- 将查询传送到数据库的时间。
- 执行本地查询片段的时间。
- 从不同站点汇集数据的时间。
- 将结果显示给应用程序的时间。
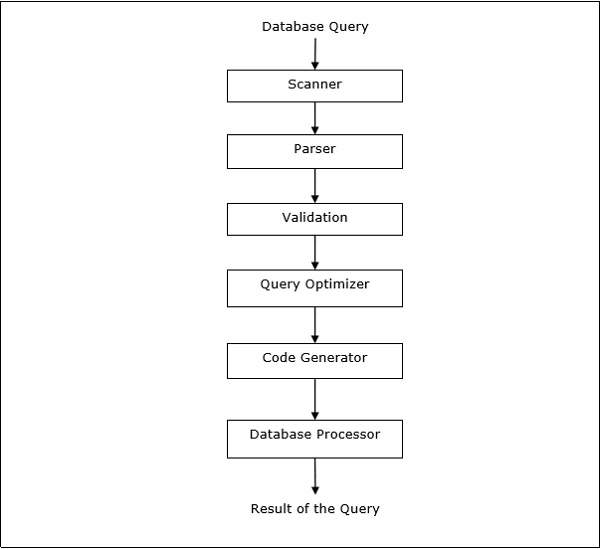
查询处理
查询处理是一组从查询放置到显示查询结果的所有活动。步骤如下面的图所示:
关系代数
关系代数定义了关系数据库模型的基本操作集。一系列关系代数操作构成一个关系代数表达式。该表达式的结果表示数据库查询的结果。
基本操作包括:
- 投影
- 选择
- 并集
- 交集
- 差集
- 连接
投影
投影操作显示表中字段的子集。这会对表进行垂直分割。
关系代数语法
$$\pi_{<{AttributeList}>}{(<{Table Name}>)}$$
例如,让我们考虑以下学生数据库:
| 学号 | 姓名 | 课程 | 学期 | 性别 |
| 2 | Amit Prasad | BCA | 1 | 男 |
| 4 | Varsha Tiwari | BCA | 1 | 女 |
| 5 | Asif Ali | MCA | 2 | 男 |
| 6 | Joe Wallace | MCA | 1 | 男 |
| 8 | Shivani Iyengar | BCA | 1 | 女 |
如果我们想显示所有学生的姓名和课程,我们将使用以下关系代数表达式:
$$\pi_{Name,Course}{(STUDENT)}$$
选择
选择操作显示满足某些条件的表中元组的子集。这会对表进行水平分割。
关系代数语法
$$\sigma_{<{Conditions}>}{(<{Table Name}>)}$$
例如,在 Student 表中,如果我们想显示所有选择了 MCA 课程的学生的详细信息,我们将使用以下关系代数表达式:
$$\sigma_{Course} = {\small "BCA"}^{(STUDENT)}$$
投影和选择操作的组合
对于大多数查询,我们需要组合投影和选择操作。有两种方法可以编写这些表达式:
- 使用投影和选择操作的序列。
- 使用重命名操作生成中间结果。
例如,要显示所有 BCA 课程的女学生的姓名:
- 使用投影和选择操作序列的关系代数表达式
$$\pi_{Name}(\sigma_{Gender = \small "Female" AND \: Course = \small "BCA"}{(STUDENT)})$$
- 使用重命名操作生成中间结果的关系代数表达式
$$FemaleBCAStudent \leftarrow \sigma_{Gender = \small "Female" AND \: Course = \small "BCA"} {(STUDENT)}$$
$$Result \leftarrow \pi_{Name}{(FemaleBCAStudent)}$$
并集
如果 P 是一个操作的结果,Q 是另一个操作的结果,则 P 和 Q 的并集($p \cup Q$)是 P 中、Q 中或两者中所有元组的集合,但不包含重复项。
例如,要显示所有在第 1 学期或选择了 BCA 课程的学生:
$$Sem1Student \leftarrow \sigma_{Semester = 1}{(STUDENT)}$$
$$BCAStudent \leftarrow \sigma_{Course = \small "BCA"}{(STUDENT)}$$
$$Result \leftarrow Sem1Student \cup BCAStudent$$
交集
如果 P 是一个操作的结果,Q 是另一个操作的结果,则 P 和 Q 的交集($p \cap Q$)是 P 和 Q 中都存在的元组的集合。
例如,给出以下两个模式:
EMPLOYEE
| EmpID | 姓名 | 城市 | 部门 | 薪资 |
PROJECT
| PId | 城市 | 部门 | 状态 |
要显示所有项目所在地和员工居住地的城市名称:
$$CityEmp \leftarrow \pi_{City}{(EMPLOYEE)}$$
$$CityProject \leftarrow \pi_{City}{(PROJECT)}$$
$$Result \leftarrow CityEmp \cap CityProject$$
差集
如果 P 是一个操作的结果,Q 是另一个操作的结果,则 P - Q 是 P 中但不在 Q 中的所有元组的集合。
例如,列出所有没有正在进行的项目的部门(状态为“正在进行”的项目):
$$AllDept \leftarrow \pi_{Department}{(EMPLOYEE)}$$
$$ProjectDept \leftarrow \pi_{Department} (\sigma_{Status = \small "ongoing"}{(PROJECT)})$$
$$Result \leftarrow AllDept - ProjectDept$$
连接
连接操作将两个不同表(查询的结果)中相关的元组组合到一个表中。
例如,考虑银行数据库中的两个模式 Customer 和 Branch,如下所示:
CUSTOMER
| CustID | AccNo | TypeOfAc | BranchID | DateOfOpening |
BRANCH
| BranchID | BranchName | IFSCcode | Address |
要列出员工详细信息以及分支详细信息:
$$Result \leftarrow CUSTOMER \bowtie_{Customer.BranchID=Branch.BranchID}{BRANCH}$$
将 SQL 查询转换为关系代数
在优化之前,SQL 查询会被转换为等效的关系代数表达式。查询首先被分解成更小的查询块。这些块被转换为等效的关系代数表达式。优化包括优化每个块,然后优化整个查询。
示例
让我们考虑以下模式:
EMPLOYEE
| EmpID | 姓名 | 城市 | 部门 | 薪资 |
PROJECT
| PId | 城市 | 部门 | 状态 |
WORKS
| EmpID | PID | Hours |
示例 1
要显示所有薪资低于平均薪资的员工的详细信息,我们编写 SQL 查询:
SELECT * FROM EMPLOYEE WHERE SALARY < ( SELECT AVERAGE(SALARY) FROM EMPLOYEE ) ;
此查询包含一个嵌套子查询。因此,可以将其分解成两个块。
内部块是:
SELECT AVERAGE(SALARY)FROM EMPLOYEE ;
如果此查询的结果为 AvgSal,则外部块为:
SELECT * FROM EMPLOYEE WHERE SALARY < AvgSal;
内部块的关系代数表达式:
$$AvgSal \leftarrow \Im_{AVERAGE(Salary)}{EMPLOYEE}$$
外部块的关系代数表达式:
$$\sigma_{Salary <{AvgSal}>}{EMPLOYEE}$$
示例 2
要显示员工“Arun Kumar”的所有项目的项目 ID 和状态,我们编写 SQL 查询:
SELECT PID, STATUS FROM PROJECT
WHERE PID = ( SELECT FROM WORKS WHERE EMPID = ( SELECT EMPID FROM EMPLOYEE
WHERE NAME = 'ARUN KUMAR'));
此查询包含两个嵌套子查询。因此,可以将其分解成三个块,如下所示:
SELECT EMPID FROM EMPLOYEE WHERE NAME = 'ARUN KUMAR'; SELECT PID FROM WORKS WHERE EMPID = ArunEmpID; SELECT PID, STATUS FROM PROJECT WHERE PID = ArunPID;
(此处 ArunEmpID 和 ArunPID 是内部查询的结果)
三个块的关系代数表达式:
$$ArunEmpID \leftarrow \pi_{EmpID}(\sigma_{Name = \small "Arun Kumar"} {(EMPLOYEE)})$$
$$ArunPID \leftarrow \pi_{PID}(\sigma_{EmpID = \small "ArunEmpID"} {(WORKS)})$$
$$Result \leftarrow \pi_{PID, Status}(\sigma_{PID = \small "ArunPID"} {(PROJECT)})$$
关系代数运算符的计算
关系代数运算符的计算可以通过多种不同的方式完成,每种备选方案称为**访问路径**。
计算备选方案取决于三个主要因素:
- 运算符类型
- 可用内存
- 磁盘结构
执行关系代数运算的时间是以下时间的总和:
- 处理元组的时间。
- 从磁盘将表的元组提取到内存的时间。
由于处理元组的时间远小于从存储中提取元组的时间,尤其是在分布式系统中,因此磁盘访问通常被视为计算关系表达式成本的指标。
选择的计算
选择操作的计算取决于选择条件的复杂性和表属性上索引的可用性。
以下是根据索引的不同计算备选方案:
**无索引** - 如果表未排序且没有索引,则选择过程涉及扫描表的全部磁盘块。每个块都被加载到内存中,并检查块中的每个元组以查看它是否满足选择条件。如果满足条件,则将其显示为输出。这是成本最高的方案,因为每个元组都被加载到内存中,并且每个元组都被处理。
**B+ 树索引** - 大多数数据库系统都建立在 B+ 树索引之上。如果选择条件基于此 B+ 树索引的键字段,则使用此索引检索结果。但是,处理具有复杂条件的选择语句可能涉及大量磁盘块访问,在某些情况下甚至需要完全扫描表。
**哈希索引** - 如果使用哈希索引并且其键字段用于选择条件,则使用哈希索引检索元组将变得非常简单。哈希索引使用哈希函数查找存储与哈希值对应的键值的桶的地址。为了在索引中查找键值,执行哈希函数并找到桶地址。搜索桶中的键值。如果找到匹配项,则从磁盘块将实际元组提取到内存中。
连接的计算
当我们想要连接两个表(例如 P 和 Q)时,必须将 P 中的每个元组与 Q 中的每个元组进行比较,以测试是否满足连接条件。如果满足条件,则连接相应的元组,消除重复字段并将其附加到结果关系。因此,这是最昂贵的操作。
计算连接的常用方法包括:
嵌套循环方法
这是传统的连接方法。可以通过以下伪代码进行说明(表 P 和 Q,元组 tuple_p 和 tuple_q,连接属性 a):
For each tuple_p in P For each tuple_q in Q If tuple_p.a = tuple_q.a Then Concatenate tuple_p and tuple_q and append to Result End If Next tuple_q Next tuple-p
排序合并方法
在这种方法中,两个表根据连接属性分别进行排序,然后将排序后的表合并。由于记录数量非常多,无法容纳在内存中,因此采用了外部排序技术。一旦各个表排序完成,将每个排序表中的一页加载到内存中,根据连接属性进行合并,并将连接后的元组写入输出。
哈希连接方法
此方法包括两个阶段:分区阶段和探测阶段。在分区阶段,表 P 和 Q 被分成两组不相交的分区。确定一个共同的哈希函数。此哈希函数用于将元组分配到分区。在探测阶段,将 P 的一个分区中的元组与 Q 的对应分区的元组进行比较。如果匹配,则将其写入输出。