数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究使用布尔模型和向量空间模型进行文档检索
简介
机器学习中的文档检索是信息检索这一更大范畴的一部分，在信息检索中，系统会尝试根据用户的查询找到与搜索查询相关的文档，并根据相关性或匹配程度对它们进行排序。
文档检索有多种方法，其中两种流行的方法是：
布尔模型
向量空间模型
让我们简要了解一下以上每种方法。
布尔模型
这是一种基于集合的检索模型。用户查询以布尔形式表示。查询使用 AND、OR、NOT 等连接。文档可以被视为一个关键字集合。根据查询，基于相关性检索文档。不支持部分匹配和排序。
示例（布尔查询）：
[[美国 & 法国] | [洪都拉斯 & 伦敦]] & 餐厅 &! 曼哈顿]
布尔模型的步骤和流程图
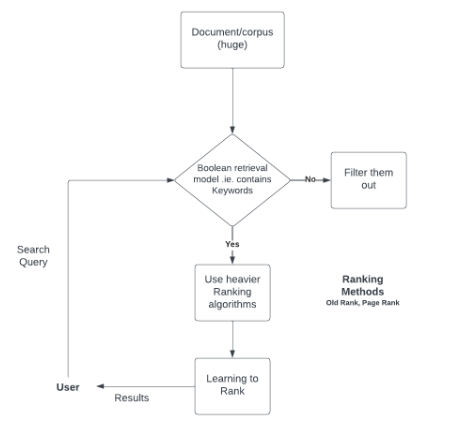
布尔模型是一种倒排索引搜索，用于查找文档是否相关。它不返回文档的排名。
假设我们的语料库中有 3 个文档。
文档ID |
文档文本 |
|---|---|
1. |
泰姬陵是一座美丽的纪念碑 |
2. |
维多利亚纪念馆也是一座纪念碑 |
3. |
我喜欢去阿格拉 |
术语矩阵将如下创建。
术语 |
doc_1 |
doc_2 |
doc_3 |
|---|---|---|---|
taj |
1 |
0 |
0 |
mahal |
1 |
0 |
0 |
is |
1 |
1 |
0 |
a |
1 |
1 |
0 |
beautiful |
1 |
0 |
0 |
monument |
1 |
1 |
0 |
victoria |
0 |
1 |
0 |
memorial |
0 |
1 |
0 |
also |
0 |
1 |
0 |
i |
0 |
0 |
1 |
like |
0 |
0 |
1 |
to |
0 |
0 |
1 |
visit |
0 |
0 |
1 |
agra |
0 |
0 |
1 |
让我们有一个像“taj mahal agra”这样的查询。
查询将创建为：
taj [100] & mahal [100] & agra [001]
或 100 & 100 & 001 = 000，因此在这里我们可以看到使用 AND 没有一个文档是相关的。
然后，我们可以尝试包含其他运算符，例如 OR，或者除了这些之外使用不同的关键字。
此语料库的倒排索引可以创建为：
taj - 集合(1) |
mahal – 集合(1) |
is - 集合(1,2) |
a - 集合(1,2) |
beautiful - 集合(1) |
monument - 集合(1,2) |
victoria – 集合(2) |
memorial - 集合(2) |
also - 集合(2) |
i - 集合(3) |
like - 集合(3) |
to - 集合(3) |
visit - 集合(3) |
agra- 集合(3) |
向量空间模型
向量空间模型是一种统计检索模型。
在此模型中，文档表示为词袋。
词袋允许单词出现多次
用户可以使用带搜索查询的权重，例如 q = < 电子商务 0.5；产品 0.8；价格 0.2
它基于查询和文档之间的相似性。
输出是排名的文档。
它还可以包含单词的多次出现。
图形表示
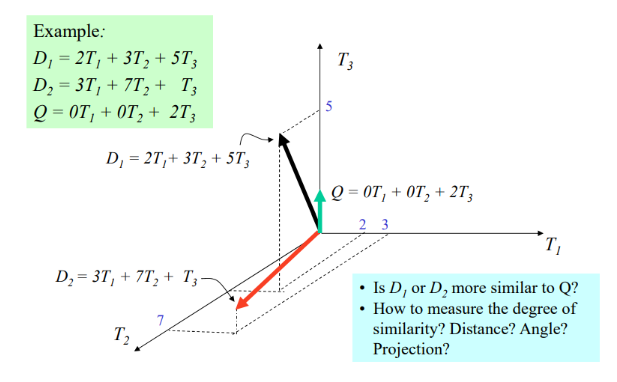
示例
import pandas as pd
from contextlib import redirect_stdout
import math
trms = []
Keys = []
vector_dic = {}
dictionary_i = {}
random_list = []
t_frequency = {}
inv_doc_freq = {}
wt = {}
def documents_filter(docs, rw, cl):
for i in range(rw):
for j in range(cl):
if(j == 0):
Keys.append(docs.loc[i].iat[j])
else:
random_list.append(docs.loc[i].iat[j])
if docs.loc[i].iat[j] not in trms:
trms.append(docs.loc[i].iat[j])
listcopy = random_list.copy()
dictionary_i.update({docs.loc[i].iat[0]: listcopy})
random_list.clear()
def calc_weight(doccount, cls):
for i in trms:
if i not in t_frequency:
t_frequency.update({i: 0})
for key, val in dictionary_i.items():
for k in val:
if k in t_frequency:
t_frequency[k] += 1
inv_doc_freq = t_frequency.copy()
for i in t_frequency:
t_frequency[i] = t_frequency[i]/cls
for i in inv_doc_freq:
if inv_doc_freq[i] != doccount:
inv_doc_freq[i] = math.log2(cls / inv_doc_freq[i])
else:
nv_doc_freq[i] = 0
for i in inv_doc_freq:
wt.update({i: inv_doc_freq[i]*t_frequency[i]})
for i in dictionary_i:
for j in dictionary_i[i]:
random_list.append(wt[j])
copy = random_list.copy()
vector_dic.update({i: copy})
random_list.clear()
def retrieve_wt_query(q):
qFrequency = {}
for i in trms:
if i not in qFrequency:
qFrequency.update({i: 0})
for val in q:
if val in qFrequency:
qFrequency[val] += 1
for i in qFrequency:
qFrequency[i] = qFrequency[i] / len(q)
return qFrequency
def compute_sim(query_Weight):
num = 0
deno1 = 0
deno2 = 0
sim= {}
for doc in dictionary_i:
for trms in dictionary_i[doc]:
num += wt[trms] * query_Weight[trms]
deno1 += wt[trms] * wt[trms]
deno2 += query_Weight[trms] * query_Weight[trms]
if deno1 != 0 and deno2 != 0:
simi = num / (math.sqrt(deno1) * math.sqrt(deno2))
sim.update({doc: simi})
num = 0
deno1 = 0
deno2 = 0
return (sim)
def pred(simi, doccount):
with open('result.txt', 'w') as f:
with redirect_stdout(f):
ans = max(simi, key=simi.get)
print(ans, "- most relevent document")
print("documents rank")
for i in range(doccount):
ans = max(simi, key=lambda x: simi[x])
print(ans, "ranking ", i+1)
simi.pop(ans)
def main():
docs = pd.read_csv(r'corpus_docs.csv')
rw = len(docs)
cls = len(docs.columns)
documents_filter(docs, rw, cls)
calc_weight(rw, cls)
print("Input your query")
q = input()
q = q.split(' ')
q_wt = retrieve_wt_query(q)
sim = compute_sim(q_wt)
pred(sim, rw)
main()
输出
Input your query
hockey
{'doc2': 0.4082482904638631}
doc2 - most relevent document
documents rank
doc2 ranking 1
结论
文档检索是如今每个搜索任务的基石。无论是搜索、数据库检索还是一般信息检索，我们都能在布尔模型和向量空间模型等模型的应用中找到答案。
6K+ 次查看
