点电荷的电势

---

介绍

很多人对“电势”这个术语感到非常困惑。在我们上学的时候，第一次听到这个词的时候，我们了解到电势与位置有一定的关系。然而，它指的是容量或强度。电势这个术语代表了电的强度。

当我们开始学习电学时，首先要面对的就是电荷。电荷是电子学的基石。它分为两种类型：正电荷和负电荷。随着我们对电荷的深入了解，我们开始认识到电场、电势、电势能、偶极子等概念。每一个单独的电荷或电荷的聚集体都有其影响范围，在这个范围内，我们可以体验到吸引力和排斥力，或者在该区域的每个位置产生电势。

什么是电势？

简单来说，我们可以说，在一个存在有效电场的区域中，某一点的电势是指我们将一个大小为1库仑的正点电荷从无限远处移动到我们所考虑的该点（该点受到持续存在的静电力影响）所需要做的功。

因此，电势也可以表示为作用在单位电荷上的功。伏特是电势的标准测量单位。因此，一个1伏特的电势点是指将一个位于无限远处的正点电荷移动到目标点所需要做的1焦耳的功。整个过程也受到电场产生的力的影响。

$$\mathrm{V=\frac{W}{q}}$$

点电荷产生的电势

我们都知道，每个电荷和多个电荷的组合都有其影响范围，称为电场。在该电场中，我们可以感受到一些静电力。点电荷也会产生电势。在下面的部分中，我们将研究点电荷产生的电势。

点电荷在检验电荷处产生的电势

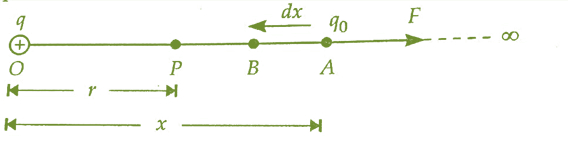
这里，一个正电荷q位于点O。现在，我们将计算距离O点r距离处的点P处的电势。根据定义，电势等于我们将一个单位正电荷从无限远处移动到我们所考虑的点P所做的功。

现在，假设在A点，距离O点x距离处有一个检验电荷$\mathrm{q_{0}}$。

利用库仑定律，我们可以计算出检验电荷由于q电荷而受到的力，

$$\mathrm{F=\frac{1}{4\pi \epsilon _{0}}.\frac{qq_{0}}{x^{2}}}$$

由于电场产生的力F的方向与$\mathrm{q_{0}}$电荷从A点移动到B点的方向相反，因此我们必须对电荷做少量功，才能使其克服q电荷产生的力，并使其发生dx位移。

因此，

$$\mathrm{dW=\overrightarrow{F}.\overrightarrow{dx}=F.dxcos\:180^{\circ}}$$

$$\mathrm{dW=-F\:dx}$$

dW 是少量功。

检验电荷从任何无限远处移动到点P所需的总功可以通过积分计算得出

$$\mathrm{W=\int dW=-\int_{\infty }^{r}F\:dx}$$

$$\mathrm{W=-\int_{\infty }^{r}\frac{1}{4\pi \epsilon _{0}}.\frac{qq_{0}}{x^{2}}\:dx}$$

$$\mathrm{W=-\frac{qq_{0}}{4\pi \epsilon _{0}}\int_{\infty }^{r}x^{-2}\:dx}$$

$$\mathrm{W=-\frac{qq_{0}}{4\pi \epsilon _{0}}\left [ -\frac{1}{x} \right ]_{\infty }^{r}}$$

$$\mathrm{W=\frac{qq_{0}}{4\pi \epsilon _{0}}\left [ \frac{1}{r}-\frac{1}{\infty } \right ]}$$

$$\mathrm{W=\frac{1}{4\pi \epsilon _{0}}.\frac{qq_{0}}{r}}$$

因此，从上述表达式可以看出，将检验电荷从无限远处移动到点P所需的功为

$$\mathrm{W=\frac{1}{4\pi \epsilon _{0}}.\frac{qq_{0}}{r}}$$

现在，我们知道电势为

$$\mathrm{V=\frac{W}{q_{0}}}$$

因此，

$$\mathrm{V=\frac{1}{4\pi \epsilon _{0}}.\frac{q}{r}}$$

多个电荷产生的电势

在这里，我们将测量由于N个电荷组成的系统在任意一点处的电势。假设系统中存在N个点电荷，即$\mathrm{q_{1},q_{2},q_{3},q_{4},q_{5},q_{6},q_{7}.....q_{N}}$。所有点电荷距离我们所考虑的点P的距离分别为$\mathrm{r_{1},r_{2},r_{3},r_{4},r_{5},r_{6},r_{7}.....r_{N}}$。

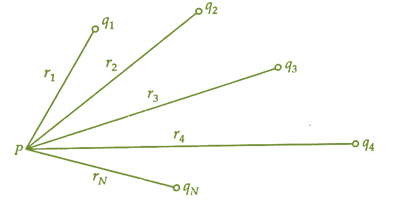
从上一节我们知道，点电荷在任意点P处的电势为

$$\mathrm{V=\frac{1}{4\pi \epsilon _{0}}.\frac{q}{r}}$$

对于电荷$\mathrm{q_{1}}$

$$\mathrm{V_{1}=\frac{1}{4\pi \epsilon _{0}}.\frac{q_{1}}{r_{1}}}$$

同样，对于其他$\mathrm{q_{1},q_{2},q_{3},q_{4},q_{5},q_{6},q_{7}.....q_{N}}$，我们得到

$$\mathrm{V_{1}=\frac{1}{4\pi \epsilon _{0}}.\frac{q_{1}}{r_{1}},V_{2}=\frac{1}{4\pi \epsilon _{0}}.\frac{q_{2}}{r_{2}},V_{3}=\frac{1}{4\pi \epsilon _{0}}.\frac{q_{3}}{r_{3}}............V_{N}=\frac{1}{4\pi \epsilon _{0}}.\frac{q_{N}}{r_{N}}}$$

我们还知道，电势不是矢量，而是标量，因此，计算N个电荷在任意点P处的总电势将是每个电荷的个体电势的总和。

因此，

$$\mathrm{V=V_{1},V_{2},V_{3},V_{4}+........+V_{N}}$$

$$\mathrm{V=\frac{1}{4\pi \epsilon _{0}}.\frac{q_{1}}{r_{1}}+\frac{1}{4\pi \epsilon _{0}}.\frac{q_{2}}{r_{2}}+\frac{1}{4\pi \epsilon _{0}}.\frac{q_{3}}{r_{3}}............+\frac{1}{4\pi \epsilon _{0}}.\frac{q_{N}}{r_{N}}}$$

$$\mathrm{V=\frac{1}{4\pi \epsilon _{0}}\left [ \frac{q_{1}}{r_{1}}+ \frac{q_{2}}{r_{2}}+\frac{q_{3}}{r_{3}}+......+\frac{q_{N}}{r_{N}}\right ]}$$

我们也可以用求和的形式写出上述方程，

$$\mathrm{V=\frac{1}{4\pi \epsilon _{0}}\sum_{i=1}^{N}\frac{q_{i}}{r_{i}}}$$

这是N个电荷系统中任意点（此处用P表示）处的总电势。

结论

在以上各节中，我们研究了单个电荷和多个电荷在任意点处的电势。我们注意到，电势是由电荷的球对称性引起的。此外，电势是标量，因此对于多个电荷，我们可以通过简单的加法计算它。

常见问题

Q1. 在任何一点，我们是否可以发现电势为零，但该点的电场不为零？

A1. 是的，我们可以找到这样的情况。我们知道，偶极子轴线上垂直方向的赤道点处的电势为零，但当我们在该点测试电场时，我们会感受到一些电场的影响。

Q2. 如果我们沿着电场线移动，电势会发生什么变化？

A2. 在这种情况下，我们会发现电势沿电场线方向减小。

Q3. 电势的标准单位的基本单位形式是什么？

A3. 电势标准单位的基本单位形式为

$$\mathrm{Potential=\frac{Work\:done}{charge}}$$

因此，

$$\mathrm{\frac{ML^{2}T^{-2}}{AT}=ML^{2}T^{-3}A^{-1}}$$

Q4. 为什么导体内部的电势是恒定的？

A4. 我们知道，电势与电场存在直接关系。任何导体内部的电场都为零，因此导体内的电势是恒定的。我们可以用以下表达式证明这一点，

$$\mathrm{E=-\frac{dV}{dr}}$$

当E = 0时

$$\mathrm{\frac{dV}{dr}=0}$$

$$\mathrm{V= Constant}$$

Q5. 等势面是什么意思？

A5. 等势面是指整个表面上每一点的电势都相等的表面。