数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法律学磁系统中存储的能量
考虑一个绕磁芯缠绕 N 匝的线圈，并连接到电压源（见图）。
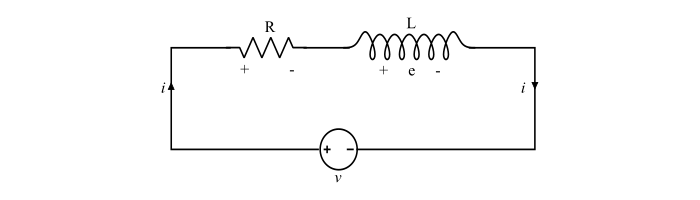
应用 KVL，得到：
$$\mathrm{V = e+iR\:\:\:\:\:\:...(1)}$$
其中：
e 是线圈中的感应电动势，
R 是线圈电路的电阻。
瞬时输入功率由下式给出：
$$\mathrm{p = Vi = e+i^{2}R\:\:\:\:\:\:...(2)}$$
因此，系统输入的能量为：
$$\mathrm{W_{i} =\int_{0}^{T}=p\:dt=\int_{0}^{T}ei\:dt+\int_{0}^{T}i^{2}Rdt\:\:\:\:\:\:...(3)}$$
等式 (3) 表明总输入能量由两部分组成。第一部分是储存在磁场中的能量，第二部分是电路电阻以热的形式耗散的能量。因此，储存在磁场中的能量由下式给出
$$\mathrm{W_{f}=\int_{0}^{T}ei\:dt}$$
此外，根据法拉第电磁感应定律，感应电动势由下式给出：
$$\mathrm{e=N\frac{dψ}{dt}=\frac{d(Nψ)}{dt}=\frac{dψ}{dt}}$$
其中，ψ = $N_{ψ}$ 是磁通链。
$$\mathrm{∴W_{f}=\int_{0}^{T}\frac{dψ}{dt}i dt=\int_{0}^{ψ}idψ\:\:\:\:\:\:...(4)}$$
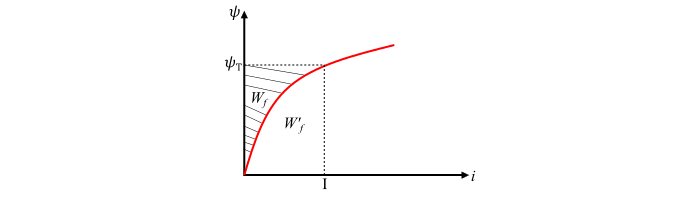
等式 (4) 表明储存在磁场中的能量等于系统 ψ-i 曲线与磁通链 (ψ) 轴之间的面积。
磁线性系统中的互能和场能
在磁线性系统中，场能由下式给出：
$$\mathrm{W_{f}=\int_{0}^{ψ}idψ}$$
$$\mathrm{\because i=\frac{ψ}{L}orψ=Li}$$
$$\mathrm{∴W_{f}=\int_{0}^{ψ}\frac{ψ}{L}dψ=\frac{ψ^{2}}{2L}}$$
$$\mathrm{\Longrightarrow W_{f}=\frac{(Li)^{2}}{2L}=\frac{1}{2}Li^{2}}$$
$$\mathrm{\Longrightarrow W_{f}=\frac{ψ^{2}}{2L}=\frac{1}{2}Li^{2}\:\:\:\:\:\:...(5)}$$
等式 (5) 中的表达式给出了储存在磁线性系统中的场能。
互能
互能是一个以能量单位测量的非物理量，用于推导电磁系统中产生的力和扭矩的表达式。互能的概念不适用于非线性系统。
对于磁线性系统，互能由下式给出：
$$\mathrm{W_{f}^{'}=\int_{0}^{i}ψdi=\int_{0}^{i}Lidi=\frac{1}{2}Li^{2}\:\:\:\:\:\:...(6)}$$
等式 (6) 表明磁线性系统中的互能等于系统 ψ-i 曲线与电流 (i) 轴之间的面积。
从等式 (5) 和 (6) 可以清楚地看出，对于磁线性系统，场能和互能相等。
$$\mathrm{W_{f}=W_{f}^{'}=\frac{ψ^{2}}{2L}=\frac{1}{2}Li^{2}\:\:\:\:\:\:...(5)}$$
3K+ 浏览量
