电容储存的能量 – 公式及示例

---

电容器是一种电子电路元件，它以静电荷的形式存储电能。因此，电容器在其内部存储势能。这种储存的电能可以在需要时获得。理想情况下，电容器不消耗能量，而是储存能量。

典型的电容器由两个金属板组成，这两个金属板之间隔着一层绝缘材料，称为介电材料。当电容器的这两个金属板连接到电源时，电容器开始充电并在其介电材料中储存电能。因此，推导出电容器中这种储存能量的表达式非常重要，这样我们就可以选择合适的电容器来进行电路设计。

电容器中储存的能量

如上所述，电容器以静电荷的形式储存电能。因此，带电电容器会产生静电场。当电容为C法拉的电容器连接到V伏特的电池上时，如图1所示。在这种情况下，整个电池电压V都加在电容器的两极板上。结果，电容器的A极板带正电，而B极板带负电。两极板之间的电位差会在电容器的介电材料中建立一个从A极板指向B极板的电场。

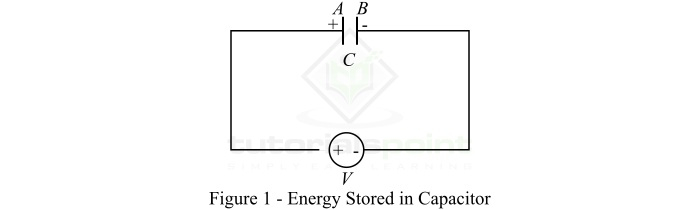
由于这种电力，介电材料靠近正极板的一端将带负极性，而靠近负极板的一端将带正极性。因此，在电容器内会产生静电荷（和静电场）。在这种情况下，据说电容器已充电并储存了有限量的能量。

现在，让我们推导出电容器中储存能量的表达式。为此，假设在充电的任何阶段，电容器中储存的电荷为q库仑，电容器两极板的电压为v伏特。那么，

$$\mathrm{q\propto v}$$

$$\mathrm{\Rightarrow q=C v}$$

根据电压的定义，在电容器中储存1库仑的电荷需要做v焦耳的功。因此，为了在电容器中储存dq库仑的电荷，所做的功是：

$$\mathrm{dW=v\, dq}$$

$$\mathrm{\Rightarrow dW=v\, d\left ( Cv \right )}$$

$$\mathrm{\therefore dW=Cv\, dv}$$

对两边积分，得到将未充电电容器的电压提高到V伏特所做的总功。

$$\mathrm{W=C\int_{0}^{v}v\, dv=C\left [ \frac{v^{2}}{2} \right ]_{0}^{v}}$$

$$\mathrm{\therefore W=\frac{1}{2}CV^{2}}$$

这项功将以势能（静电场）的形式储存在电容器中。

此外，

$$\mathrm{C=\frac{Q}{V}\: and\: V=\frac{Q}{C}}$$

因此，电容器中储存的能量也可以表示为：

$$\mathrm{W=\frac{1}{2}QV=\frac{1}{2}\frac{Q^{2}}{C}}$$

如果电荷Q以库仑为单位给出，C以法拉为单位，V以伏特为单位，则电容器中储存的能量将以焦耳表示。

从电容器储存能量的公式可以看出，电容器储存的能量与流过电容器的电流无关。

注意 – 纯电容器或理想电容器不消耗能量，而是储存能量，并在向电路供电时返回储存的能量。

数值示例（1）

一个电容为0.5 μF的电容器连接到120 V的电池上。确定电容器中储存的能量。

解答

给定数据：

• 𝐶 = 0.5 μF = 0.5 × 10⁻⁶F
• 𝑉 = 120 V

电容器中储存的能量为：

$$\mathrm{W=\frac{1}{2}CV^{2}=\frac{1}{2}\times \left ( 0.5\times 10^{-6} \right )\times 120^{2}}$$

$$\mathrm{\therefore W=3.6\times 10^{-3}J=3.6\, mJ}$$

数值示例（2）

当电容器连接到240 V的电源时，它储存了50 mC的电荷。计算电容器中储存的能量。

解答

给定数据：

• 电压，𝑉 = 240 V
• 电荷，𝑄 = 50 mC = 50 × 10⁻³ C

电容器中储存的能量由下式给出：

$$\mathrm{W=\frac{1}{2}QV=\frac{1}{2}\times \left ( 50\times 10^{-3} \right )\times 240}$$

$$\mathrm{\therefore W=6\, Joules}$$

结论

从上面的讨论可以看出，电容器以静电场形式储存电能，这种储存的能量被称为势能，因为它是由电位差引起的。

从电容器储存能量的表达式可以看出，储存的能量与电容器的电容成正比，这意味着对于相同的电压，电容更大的电容器可以储存更多的能量，反之亦然。

由于其储能特性，电容器被广泛应用于各种电气和电子电路中，例如充电器、电容器组、计算机电路等。