电容的充电 – 公式、图表和示例

---

电容是电气和电子电路中使用的无源电路元件，用于引入电容。电容定义为物质的一种属性，它以静电场的形式存储电能。

典型的电容由两个金属极板组成，这两个极板由介电材料隔开。正是这种介电材料能够以静电荷的形式存储电能。

当电容连接到电源时，以静电场形式存储电能的过程称为电容的充电。这种储存在静电场中的能量可以在以后的时间点传递到电路。

在本文中，我们将讨论电容的充电，并将推导出充电过程中电容中存储的电压、电流和电荷的方程式。

什么是电容的充电？

如前所述，电容的充电是将能量以静电荷的形式存储在电容介电介质中的过程。

考虑一个未充电的电容，其电容为 C 法拉。该电容通过电阻 R 和开关 S 连接到 V 伏特的直流电压源，如图 1 所示。

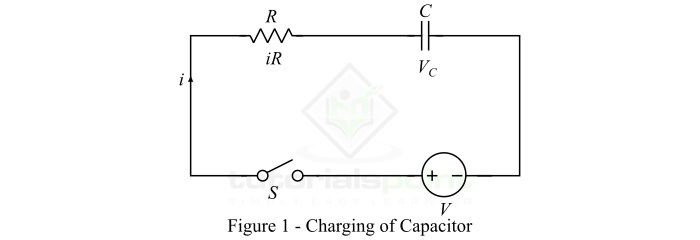
当开关 S 关闭时，电容开始充电，即充电电流开始流过电路。该充电电流在开关瞬间最大，并随着电容两端的电压逐渐增大而逐渐减小。一旦电容充电到等于电源电压 V 的电压，充电电流将变为零。

因此，为了理解电容的充电，我们考虑以下两个时刻：

时刻 1 - 开关闭合时

在开关瞬间，电容两端的电压为零，因为我们最初使用的是完全放电的电容。在这个时刻，整个电源电压 V 降落在电阻 R 上，充电电流最大（例如 I_m）。

因此，

$$\mathrm{初始充电电流，I_{m}=\frac{V}{R}}$$

$$\mathrm{电容两端的电压，V_{C} = 0}$$

$$\mathrm{电容上的电荷，Q_{C} = 0}$$

时刻 2：任意时刻“t”

关闭开关 S 后，电容两端的电压开始增加，电路中的充电电流开始逐渐减小。设在电容充电过程中的任意时刻 t，

$$\mathrm{充电电流 = i}$$

$$\mathrm{电容两端的电压，V_{C} = v}$$

$$\mathrm{电容上的电荷，Q_{C} = q = Cv}$$

现在，在电路中应用基尔霍夫电压定律，我们可以写出：

$$\mathrm{V=v+iR\: \cdot \cdot \cdot (1)}$$

$$\mathrm{\因为电容中的电流，i=C\frac{dv}{dt}}$$

$$\mathrm{\所以 V=v+CR\frac{dv}{dt}}$$

重新排列方程式，我们得到：

$$\mathrm{\frac{dv}{V-v}=\frac{dt}{RC}}$$

对两边积分，我们得到：

$$\mathrm{\int \frac{dv}{V-v}=\int \frac{dt}{RC}}$$

$$\mathrm{\因为 \int \frac{dx}{1-x}=-log_{e}\left|1-x \right|}$$

使用这个积分恒等式，我们得到：

$$\mathrm{-log_{e}\left ( V-v \right )=\frac{t}{RC}+K}$$

其中，K 是一个常数，其值可以由电容的初始条件确定。因此，在 t = 0 时，v = 0。

$$\mathrm{\所以 K=-log_{e}V }$$

将 K 的这个值代入上述表达式，我们得到：

$$\mathrm{-log_{e}\left ( V-v \right )=\frac{t}{RC}-log_{e}V}$$

$$\mathrm{\Rightarrow log_{e}\left ( V-v \right )-log_{e}V=-\frac{t}{RC}}$$

$$\mathrm{\Rightarrow log_{e}\left ( \frac{V-v}{V} \right )=-\frac{t}{RC}}$$

对两边取反对数，我们得到：

$$\mathrm{\Rightarrow \frac{V-v}{V}=e^{-\frac{t}{RC}}}$$

重新排列这个方程式，我们得到：

$$\mathrm{v=V\left ( 1-e^{-\frac{t}{RC}} \right )\: \cdot \cdot \cdot \left ( 2 \right )}$$

公式 (2) 中的表达式给出了任意时刻 t 时的电容两端的电压。它表明电容在充电过程中电压的增加遵循指数规律。

公式 (2) 还表明，随着 t 的增加，指数项 e^-t/RC 减小，电容两端的电压增加。当项 e^-t/RC 变为零时，电容两端的电压将等于电源电压 V，并且据说电容已完全充电。当电容完全充电时，电阻 R 上的电压降为零。

电容上的电荷

如果电容在任意时刻 t 的电荷为 q，并且当电容完全充电时为 Q。对于电容，我们有：

$$\mathrm{v=\frac{q}{C}\: 和\: V=\frac{Q}{C}}$$

然后，从公式 (2)，我们有：

$$\mathrm{\frac{q}{C}=\frac{Q}{C}\left ( 1-e^{-\frac{t}{RC}} \right )}$$

$$\mathrm{\所以 q=Q\left ( 1-e^{-\frac{t}{RC}} \right )\: \: \cdot \cdot \cdot \left ( 3 \right )}$$

这表明电容极板上的电荷在充电过程中呈指数增长。

电容的充电电流

从公式 (1)，我们有：

$$\mathrm{V-v=iR\: \: \cdot \cdot \cdot \left ( 4 \right )}$$

从公式 (2)，我们有。

$$\mathrm{V-v=Ve^{-\frac{t}{RC}}\: \: \cdot \cdot \cdot \left ( 5 \right )}$$

因此，

$$\mathrm{iR=Ve^{-\frac{t}{RC}}}$$

$$\mathrm{\Rightarrow i=\frac{V}{R}e^{-\frac{t}{RC}}}$$

$$\mathrm{\所以 i=I_{m}e^{-\frac{t}{RC}}\: \: \cdot \cdot \cdot \left ( 6 \right )}$$

其中，I_m 是初始充电电流。从公式 (6) 可以看出，电容的充电电流在电容的充电过程中呈指数衰减。

电容充电的图形表示

电容充电电压和电流的图形表示如图 2 所示。

数值示例

一个 5 μF 的电容与一个 1 MΩ 的电阻串联，连接到 250 V 的电源上。计算：初始充电电流，以及连接到电源 5 秒后电容上的充电电流和电压。

解答

已知数据：

• 电容，C = 5 μF
• 串联电阻，R = 1 MΩ
• 电源电压，V = 250 V

初始充电电流

$$\mathrm{I_{m}=\frac{V}{R}=\frac{250}{1}=250\, \mu A}$$

5 秒后的充电电流

$$\mathrm{i=I_{m}e^{\frac{t}{RC}}=250\times e^{\left ( \frac{-5}{1\times 10^{6}\times 5\times10^{-6}} \right )} }$$

$$\mathrm{i=250\times 0.367=91.75\, \mu A }$$

5 秒后电容两端的电压

$$\mathrm{v=V\left ( 1-e^{-\frac{t}{RC}} \right )}$$

$$\mathrm{\Rightarrow v=250 \left [ 1-e^{\left ( \frac{-5}{1\times 10^{6}\times 5\times10^{-6}} \right )} \right ] }$$

$$\mathrm{\Rightarrow v=250 \times 0.633 = 158.25 V }$$

结论

从以上讨论可以得出结论，在电容充电过程中，电容两端的电荷和电压呈指数增长，而充电电流呈指数衰减。带电电容以静电荷的形式在电容极板之间的介电介质中存储电能。