电感和电容的品质因数

---

作为振荡系统（例如交流电路）的一个参数，它表示存储能量和能量耗散之间的关系，被称为系统的品质因数。品质因数也称为Q值。

从数学上讲，交流电路的品质因数或Q值由电路中存储的最大电能与一个周期内耗散的能量之比给出，即：

$$\mathrm{ Q \: 因数 =\frac{2\pi \times 每周期最大储存能量}{每周期耗散能量} } $$

只有包含储能元件的电路才能定义品质因数（Q值）。在交流电路中，有两个储能元件，即电感和电容。因此，在本文中，我们将讨论电感和电容的品质因数。

电感的品质因数

电感是一种无源电路元件，它以磁场的形式存储电能。电感存储磁场能量的特性称为电感。

电感是通过将导线缠绕成线圈来制造的。理想情况下，电感应具有非常高的电感和零电阻，但实际电感除了电感外还具有小的电阻。因此，为了获得更好的品质电感，电感电阻的值应尽可能低。

电感电阻值低和电感值高表示电感每周期存储的最大能量大于每周期耗散的能量。这样的电感具有高品质因数。

对于给定的工作频率，电感的品质因数或Q值定义为电感中存储的最大能量与每周期耗散的能量之比，即：

$$\mathrm{ Q \: 因数 =\frac{I^{2}X_{L}}{I^{2}R}=\frac{X_{L}}{R} =\frac{\omega L}{R}} $$

其中，L是电感的电感，R是电感的电阻。

因此，电感的品质因数由电抗除以电感电阻给出。

品质因数是无量纲量

X_L和R的单位相同，即欧姆。因此，品质因数是无量纲量。

现在，让我们证明上述电感品质因数的表达式。

考虑一个具有L亨利电感和R欧姆电阻的电感。它连接到一个V伏交流电压源，其角频率为ω弧度/秒。设电路中的最大电流为I_m。

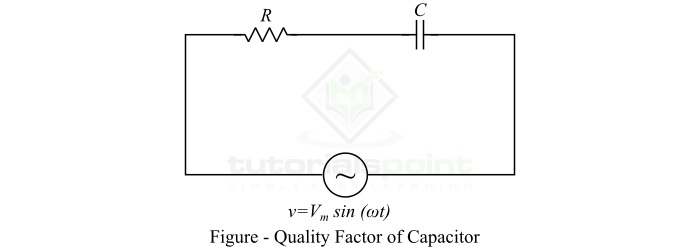
则电感中存储的最大能量由下式给出：

$$\mathrm{W_{m}=\frac{1}{2}LI_{m}^{2}}$$

此外，由于电感电阻在一个周期内在电感中耗散的能量由下式给出：

$$\mathrm{W_{d}=\left ( \frac{I_{m}}{\sqrt{2}} \right )^{2}\, RT=\left ( \frac{I_{m}}{\sqrt{2}} \right )^{2}\times R\times \frac{1}{f}}$$

其中，T是交流电压的周期。

因此，根据品质因数的定义，我们得到：

$$\mathrm{Q\: 因数=\frac{2\pi \times \left ( \frac{1}{2}LI_{m}^{2} \right )}{\left ( \frac{I_{m}}{\sqrt{2}} \right )^{2}\times R\times \frac{1}{f}}}$$

$$\mathrm{\Rightarrow Q\: 因数=\frac{2\pi fL}{R}=\frac{\omega L}{R}= \frac{X_{L}}{R}}$$

因此，这就是电感的品质因数。

电容的品质因数

电容也是一种电路元件，它以静电能的形式存储电能。理想电容的电阻应为零，电容应非常高。但是，实际电容除了电容外还具有小的电阻。为了获得更好的电容品质，该电阻的值应更低。

电容设计用于存储能量，但由于内部电阻，它还会耗散一部分输入能量。提供有关电容质量信息的参数称为电容的品质因数。

对于ω rad/sec的工作频率，电容的品质因数定义为存储的最大能量与在一个周期内在电容中耗散的能量之比，即：

$$\mathrm{Q\: 因数=\frac{I^{2}X_{c}}{I^{2}R}=\frac{X_{c}}{R}=\frac{1}{\omega CR}}$$

其中，𝑋_𝐶是容抗，R是电容的电阻。

考虑一个具有C法拉电容和R欧姆电阻的电容。它连接到一个V伏交流电压源。

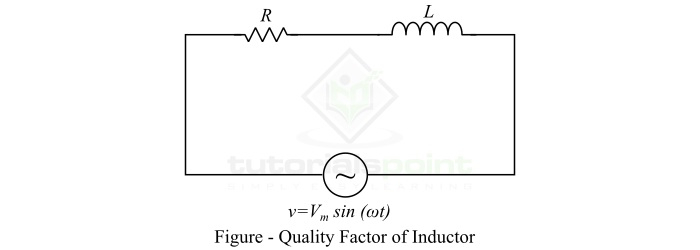
如果𝑉_𝑚是电源电压的最大值，则电容中存储的最大能量由下式给出：

$$\mathrm{W_{m}=\frac{1}{2}CV_{m}^{2}}$$

但是，R << X_C，因此：

$$\mathrm{V_{m}=I_{m}X_{c}=\frac{I_{m}}{\omega C}}$$

因此，每周期在电容中存储的最大能量由下式给出：

$$\mathrm{W_{m}=\frac{1}{2}\left ( \frac{I_{m}^{2}}{\omega ^{2}C} \right )}$$

而且，由于电容电阻在一个周期内在电容中耗散的能量由下式给出：

$$\mathrm{W_{d}=\left ( \frac{I_{m}}{\sqrt{2}} \right )^{2}\,RT=\left ( \frac{I_{m}}{\sqrt{2}} \right )^{2} R\times \frac{1}{f}}$$

因此，电容的品质因数将为：

$$\mathrm{Q\: 因数=2\pi \times \left [ \frac{\frac{1}{2}\left ( \frac{I_{m}^{2}}{\omega ^{2}C} \right )}{\left ( \frac{I_{m}}{\sqrt{2}} \right )^{2}\, R\times \frac{1}{f}} \right ]=\frac{1}{\omega RC}=\frac{X_{C}}{R}}$$

因此，这就是电容的品质因数。

数值例子 (1)

一个具有2 mH电感和1 Ω电阻的实际电感连接到一个50 Hz频率的交流电压源。确定电感的品质因数。

解答

给定数据：

• 电感，𝐿 = 2 mH = 2 × 10⁻³H
• 电阻，𝑅 = 1 Ω
• 频率，𝑓 = 50 Hz

因此，电感的品质因数为

$$\mathrm{Q\: 因数=\frac{2\pi fL}{R}=\frac{2\pi \times 50\times 2\times 10^{-3}}{1}=0.628}$$

数值例子 (2)

一个3 μF的电容具有1.5 Ω的电阻，并连接到一个50 Hz频率的交流电源。确定电容的品质因数。

解答

给定数据：

• 电容，𝐶 = 3 μF = 3 × 10⁻⁶ F
• 电阻，𝑅 = 1.5 Ω
• 频率，𝑓 = 50 Hz

因此，电容的品质因数由下式给出：

$$\mathrm{Q\: 因数=\frac{1}{2\pi fRC}=\frac{1}{2\pi \times 50\times 1.5\times3\times 10^{-6}}}$$

$$\mathrm{\therefore Q\: 因数=0.001413}$$

结论

从以上讨论中，我们可以得出结论：如果电阻远小于其电抗电感，则电感将具有高品质因数。电感的高品质因数表明它将在交流电源的一个周期内存储更多能量并耗散更少能量。

同样，如果电容的容抗大于其电阻，则认为电容具有高品质，以便它仅耗散少量能量。