交流电压加在电感器上

---

介绍

交流电压是由交流电引起的。当载流导体在磁场中旋转时，磁通量的变化会在线圈中感应出交流电压。这被称为感应电动势。电感器是一个线圈，当交流电通过它时会在其中感应出反电动势。这种反电动势产生一个与交流输入相反的电流。

交流电压

交流电(AC) 定义为定期改变其方向和大小的电流。因此，交流电压是交流电流流经的端子之间的电压差。数学上，交流电压和交流电流可以表示为

$$\mathrm{V(t)=V_0\:sin(\omega t)}$$

$$\mathrm{I(t)= I_0\:sin(\omega t)}$$

电感器

电感器是一种无源电子元件，它通过将电能转换为磁能来存储能量。电感器是由绝缘导线绕成的线圈，当流过它的电流发生变化时，它的磁场也会发生变化。从而感应出电动势。这个感应电动势会阻碍电路中电流的流动。楞次定律指出，电路中产生的感应电动势总是与流过它的电流方向相反。根据此定律，感应电动势为：

$$\mathrm{V =- L\frac{di}{dt}}$$

其中 i=电源电流，L 是线圈的电感

电感 (L) 及其类型

电路中感应电动势与电流随时间变化率之比称为线圈的电感。电感可分为两种：

• 自感

• 互感

自感

如果通过线圈的电流随时间变化，则与线圈相关的磁通量也会发生变化，因此会在电路本身中感应出电动势。这称为自感。

互感

假设通过初级线圈的电流发生变化，则与线圈相关的磁通量也会发生变化。这种变化会引起次级线圈磁通量的变化，从而在次级电路中感应出电动势。这称为互感。两者都是由于通过线圈的电流发生变化而导致线圈相关的磁通量发生变化而产生的。亨利 (H) 是电感的单位。

带有交流偏置的电感器

这可以用一个简单的电路轻松描述。在交流电路中，电感器、灯泡和开关串联连接。当连接开关时，交流电流流过它，但灯泡不会突然亮起。它会缓慢变亮。因为在此期间，感应电流会阻碍电源电流的增长。当断开开关时，灯泡不会突然熄灭。因为电路中产生的感应电动势会阻碍电源电流的衰减。在直流电路中，这种阻碍因素定义为电阻。但在交流电路中，它被称为阻抗。

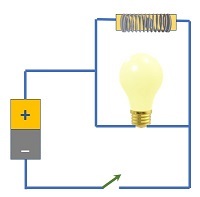
交流电压加在电感器上

如果将交流电压加在电感器上，则磁力线会发生变化，进而与线圈相关的磁通量也会发生变化，从而感应出与电感器电流流动方向相反的电动势。这种对电流流动的阻碍是由于线圈的交流电阻引起的。这也被称为感抗 $\mathrm{X_L}$

$$\mathrm{X_L = \omega L}$$

$$\mathrm{X_L = 2\pi fL}$$

https://lizenzhinweisgenerator.de/?lang=en&url=/wiki/File:Sydney_(AU),_Coast,_New_Zealand_sea_lions_--_2019_--_3489.jpg

通常，交流电压表示为：

$$\mathrm{V(t) = V_0\:sin(\omega t)}$$

$$\mathrm{\omega= 角频率}$$

$$\mathrm{V_0= 最大电压}$$

根据法拉第电磁感应定律，感应电动势表示为：

$$\mathrm{V=-L\frac{di}{dt}}$$

当电流通过电感器时，感应电动势会阻碍电流的流动。电源电压必须等于反电动势才能保持电流平衡。

$$\mathrm{L\frac{di}{dt}=V_0 \:sin(\omega t)}$$

$$\mathrm{\frac{di}{dt}=\frac{V_0 sin(\omega t)}{L}}$$

$$\mathrm{\int \frac{di}{dt}=\frac{V_0}{L}\int sin(\omega t)}$$

(由于 V0 和 L 为常数，因此它们从积分中提出)

积分该方程，我们得到：

$$\mathrm{i=\frac{V_0}{L}(−cos(\omega t)/ \omega)}$$

$$\mathrm{i =\frac{V_0}{L\omega}(−cos \:\omega t) + C}$$

为了找到 C 的值：

如果 $\mathrm{V_0=0}$，则 i=0，这意味着 C=0，因此

$$\mathrm{i =\frac{V_0}{L\omega}(−cos \:\omega t)}$$

$\mathrm{cos\omega t}$ 可以写成 $\mathrm{sin(90^{\circ}-\omega t)}$

将负号插入 -cosωt 将变为 $\mathrm{sin\:(\omega t- 90^{\circ})}$

这可以修改为：

$$\mathrm{i =\frac{V_0}{L\omega}(sin(\omega t−90^{\circ}))}$$

$$\mathrm{i =\frac{V_0}{X_L}(sin(\omega t−90^{\circ}))}$$

$$\mathrm{i =i_0(sin(\omega t−90^{\circ}))\:\:\:\:\:(as\:\:\frac{V_0}{X_L}=i_0)}$$

$$\mathrm{X_L = L\omega}$$

$\mathrm{X_L}$ = 线圈的感抗

感抗的 SI 单位是欧姆。

$\mathrm{i_0}$ = 最大电流

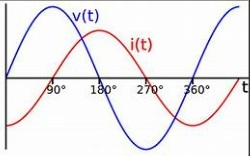
因此，电感器电路中的电流滞后于电压 90 度。

交流电路中的功率

电路中的功率会随着电路中电压和电流的变化而不断变化。电感器电路中的功率为

$$\mathrm{P = VI}$$

如果电压和电流之间存在相位差，则：

$$\mathrm{V(t) = V_0 \:sin(\omega t)}$$

$$\mathrm{I(t) = I_0 \:sin(\omega t-\Phi)}$$

因此功率

$$\mathrm{P = V_0 I_0 \:sin(\omega t-\Phi) sin(\omega t)}$$

因为

$$\mathrm{sinA\:sinB=\frac{1}{2}cos(A-B)-cos(A+B)}$$

$$\mathrm{P=\frac{V_0 I_0}{2}(cos \Phi - cos(2\omega t- \Phi))}$$

平均功率

$$\mathrm{P_{avg}=\frac{V_0 I_0}{2}(\int\: cos⁡\:\Phi- cos(2\omega t-\Phi) )}$$

$$\mathrm{P_{avg}=\frac{V_0 I_0}{2}cos\: \Phi\:\:\:(通过代入极限\: cos(2\omega t-\Phi)=0)}$$

$$\mathrm{P_{avg}=\frac{V I}{2}cos\:\Phi}$$

对于纯电感，如果相位差为

$$\mathrm{\Phi=\frac{\pi}{2}\:\:则\:\:cos\frac{\pi}{2}=0}$$

因此功率 $\mathrm{P=0}$

功率因数

交流电路中的功率因数是视在功率与实际功率之比。

$$\mathrm{功率因数=\frac{视在功率}{有功功率}}$$

结论

交流电的大小和方向会定期变化。这种交流电的变化会改变与连接到电源的线圈相关的磁通量，从而在线圈中感应出与电路电流方向相反的电动势。

在施加交流电压的电感器电路中，电流滞后于电压 90 度。这取决于施加电压的电压和频率。对于纯电感，消耗的功率为零。因为电压和电流之间的相位差为零。

常见问题

Q1. 电感为 1.5H 的电感器在 50Hz 的频率下工作。计算其感抗？

答：感抗为 $\mathrm{X_L=2\Pi fL}$

$$\mathrm{X_L = 2 \times 3.14 \times 50 \times 1.5}$$

$$\mathrm{X_L = 471\Omega}$$

因此，电感器的感抗为 $\mathrm{471\Omega}$。

Q2. 纯电感电路中电压和电流之间的关系是什么？

答：在纯电感电路中，电流滞后于电压 90 度。

Q3. 用数学方法表示交流电流和交流电压。

答：交流电定义为定期改变其方向和大小的电流。因此，交流电压是交流电流流经的端子之间的电压差。数学上，交流电压和交流电流可以表示为：

$$\mathrm{V(t)= V_0\:sin(\omega t)}$$

$$\mathrm{I(t)= I_0 sin(\omega t)}$$

Q4. 电感器中会发生什么，它的电压是多少？

答：电感器是由绝缘导线绕成的线圈，当通过它的电流发生变化时，它的磁场也会发生变化，从而在其与电流流动方向相反的方向上感应出电动势。该感应电动势始终与流过电路的电流方向相反。电感器电压为

$$\mathrm{V=L\frac{di}{dt}}$$

Q5. 定义电感及其单位是什么？

答：电路中感应电动势与电流随时间变化率之比称为线圈的电感。电感的单位是亨利 (H)。

Q6. 什么是电磁感应？

答：电感器是由绝缘导线绕成的线圈，当流过它的电流发生变化时，它的磁场也会发生变化，从而感应出电动势。该感应电动势会阻碍电流通过电路。这称为电磁感应，它由法拉第很好地定义。

Q7. 什么是楞次定律？

答：由于通过电路的交流电流变化而产生的感应电动势总是与流过它的电流方向相反。