变压器电压降近似值和变压器电压调整率

变压器电压降近似值

图示为实际变压器折算到副边上的近似等效电路。

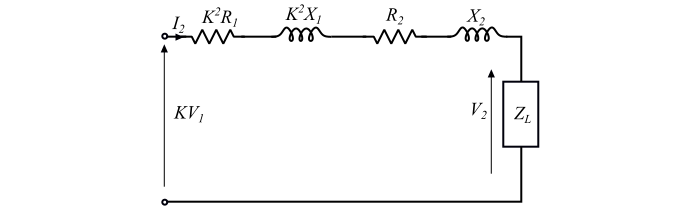
空载时，即 I₂= 0，副边端电压为：

$$\mathrm{V_{2}=KV_{1} .....(1)}$$

当连接功率因数为 cosφ2（滞后）的感性负载到变压器的副绕组时，副绕组流过电流 I₂，因此在 $(R_{2} + K^2R_{1})$ 和 $(X_{2} + K^2X_{1})$ 上产生电压降。结果，副边电压从 KV₁ 降到负载端子上的 V₂。

根据基尔霍夫电压定律 (KVL)，我们得到：

$$\mathrm{V_{2}=KV_{1}-I_{2}[(R_{2} + K^2R_{1})+J(X_{2} + K^2X_{1})]}$$

$$\mathrm{⇒ V_{2}=KV_{1}-I_{2}(R_{02} +jX_{02}) = KV_{1}-I_{2}Z_{02}}$$

因此，副边电压降为：

$$\mathrm{ KV_{1}-V_{2}=I_{2}Z_{02} .....(2)}$$

现在，参考相量图，可以看出副边电压降为 $AC = I_{2}Z_{02}$，其计算方法如下：

以 O 为圆心，OC 为半径，画弧 OA 并延长至 M，则：

$$\mathrm{AC=AM \approx AN}$$

现在，从 B 作 BD 垂直于 OA，作 CN 垂直于 OM，作 BL 平行于 OM。因此，副边电压的近似降压由下式给出：

$$\mathrm{副边电压近似降压= AN = AD+DN}$$

$$\mathrm{\therefore \:BL = DN}$$

$$\mathrm{\because \:AN = AD + BL}$$

$$\mathrm{⇒ AN = I_{2}R_{02}\:cos\:\varphi _{2}\: + I_{2}X_{02}\:sin\:\varphi _{2} ....(3)}$$

公式 (3) 给出了滞后功率因数负载的副边电压近似降压。

对于 *超前功率因数* 负载，变压器的近似电压降由下式给出：

$$\mathrm{近似电压降\:=I_{2}R_{02}\:cos\:\varphi _{2}\:-\:I_{2}X_{02}\:sin\:\varphi _{2} ....(4)}$$

此外，如果变压器电路折算到原边，则

$$\mathrm{近似电压降\:= I_{1}R_{01}\:cos\:\varphi_{1}\:±\:I_{1}X_{01}\:sin\:\varphi _{1} ....(5) }$$

由于原边功率因数 (cos φ1) 和副边功率因数 (cos φ2) 的值差异很小。因此，公式 (5) 也可以写成

$$\mathrm{近似电压降\:=\:I_{1}R_{01}\:cos\:\varphi _{2}\: ±\:I_{1}X_{01}\:sin\:\varphi _{2} ....(6)}$$

这里，对于滞后功率因数负载使用正号，对于超前功率因数负载使用负号。

变压器电压调整率

变压器的电压调整率定义为空载副边端电压 (V_2NL) 与满载副边端电压 (V_2FL) 之间的算术差，以给定功率因数下满载（额定）副边端电压的百分比表示，原边电压在空载和满载时保持恒定值，即

$$\mathrm{电压调整率\:= \frac{V_{2NL}\:-\:V_{2FL}}{V_{2FL}}\:*100 ..... (7) }$$

从公式 (2) 可知，空载副边端电压为

$$V_{2NL} = KV_{1}$$

因此，变压器从空载到满载的电压降由下式给出：

$$\mathrm{V_{2NL}\:-\:V_{2FL}\:=\: I_{2}R_{02}\:cos\:\varphi _{2}\:±\:I_{2}X_{02}\:sin\:\varphi _{2} .....(8)}$$

其中，滞后功率因数负载使用正号，超前功率因数负载使用负号。

$$\mathrm{\therefore\:电压调整率\:=\:\frac{I_{2}R_{02}\:cos\:\varphi_{2}\:±\:I_{2}X_{02}\:sin\:\varphi _{2}}{V_{2FL}} ......(9)}$$

电压调整率是衡量变压器性能的指标。对于理想变压器，电压调整率为零。为了使变压器更好地运行，电压调整率应尽可能小。

对于变压器，电压变化的限值以电压调整率的形式规定。例如，用于公共供电系统的变压器的端电压变化不得超过 ± 5%。

零电压调整率的条件

考虑连接到变压器上的感性负载，则变压器的电压调整率为

$$\mathrm{\therefore\:电压调整率\:=\:\frac{I_{2}R_{02}\:cos\:\varphi _{2}\:+\:I_{2}X_{02}\:sin\:\varphi _{2}}{V_{2FL}} ..... (9)}$$

从这个表达式可以看出，当分子为零时，电压调整率将为零，即

$$\mathrm{I_{2}R_{02}\:cos\:\varphi _{2}\:+\:I_{2}X_{02}\:sin\:\varphi_{2}= 0}$$

$$\mathrm{⇒\:tan\:\varphi_{2}\:=\:-\frac{R_{02}}{X_{02}}}$$

$$\mathrm{⇒\:\varphi_{2}\:=\:-tan^-1(\frac{R_{02}}{X_{02}}) .....(10)}$$

这里，负号表示当负载为容性，即具有超前功率因数时，会发生零电压调整率。

Saini Manish Kumar

更新于：2021年8月12日

浏览量：1000+

开启你的职业生涯

完成课程获得认证

开始学习