Potier三角形法 - 确定同步发电机的电压调整

Potier三角形法用于确定同步发电机的电压调整。它也称为零功率因数 (ZPF) 法。在Potier三角形法中做出了以下假设：

• 电枢反应磁动势是恒定的。

• 空载时测得的开路特性 (O.C.C.) 精确地表示了负载条件下磁动势和电压之间的关系。

• 电枢漏抗引起的电压降 ($𝐼_{𝑎}𝑋_{𝑎𝐿}$) 与励磁无关。

使用 ZPF 方法获取电压调整的程序

以下是使用零功率因数 (ZPF) 方法确定同步发电机或交流发电机电压调整的程序：

首先，我们绘制同步发电机在滞后功率因数下的相量图，如图所示。

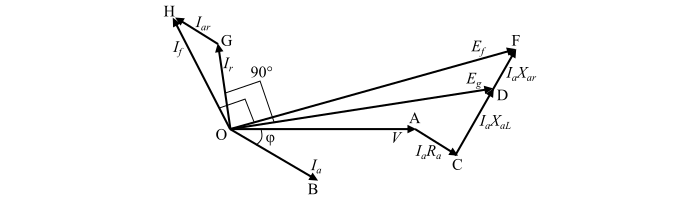
在相量图中，

• 相量 OA 表示满载时的端相电压 (V)。它被视为参考相量，因此水平绘制。

• 相量 OB 表示满载电流 ($𝐼_{𝑎}$)。由于负载功率因数为 φ 滞后，因此它以功率因数角 (φ) 滞后于电压 (V) 绘制。

• 相量 AC 表示电枢电阻中的电压降 ($𝐼_{𝑎}𝑅_{𝑎}$)。由于它与电枢电流 ($𝐼_{𝑎}$) 同相，因此平行于电流相量 ($𝐼_{𝑎}$) 绘制。如果忽略电枢电阻，则该相量将不会在相量图中绘制。

• 由于漏抗引起的电压降 ($𝐼_{𝑎}𝑋_{𝑎𝐿}$) 由相量 CD 表示。它垂直于相量 AC。

• 现在，连接 O 和 D，相量 OD 表示感应电动势 ($𝐸_{𝑔}$)。

现在，从开路特性 (O.C.C.) 中找到对应于感应电动势 ($𝐸_{𝑔}$) 的合成磁动势的励磁电流 ($𝐼_{𝑟}$)。然后，绘制等于电流 ($𝐼_{𝑟}$) 的相量 OG，它垂直于相量 OD。

绘制平行于负载电流 ($𝐼_{𝑎}$) 的相量 GH，以表示等效于满载电枢反应电流 ($𝐼_{a𝑟}$) 的励磁电流。因此，相量 OH 给出了总励磁电流 ($𝐼_{𝑓}$)。

当同步发电机的负载断开时，端电压将等于对应于励磁电流 ($𝐼_{𝑓} = 𝑂𝐻$) 的感应电动势。

现在，从 O.C.C. 中确定对应于励磁电流 ($𝐼_{𝑓} = 𝑂𝐻$) 的相量 OF 所表示的电动势 ($𝐸_{𝑓}$)。相量 OF 将滞后于相量 OH 90°。此外，由于电枢反应引起的电压降由相量 DF 表示。

因此，同步发电机或交流发电机的电压调整可以通过以下表达式获得：

$$\mathrm{\%\:电压调整 =\frac{𝐸_{𝑓} − 𝑉}{𝑉} \times 100}$$

Manish Kumar Saini

更新于: 2021-10-18

7K+ 次查看

开启您的 职业生涯

通过完成课程获得认证

开始学习