数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会研究
服装研究
法律研究同步发电机–零功率因数特性和Potier三角形
零功率因数特性(ZPFC)是当机器以同步速度和零滞后功率因数运行时，每相电枢端电压和励磁电流之间绘制的曲线图。ZPFC也称为Potier特性，以其创始人命名。
为了使功率因数保持非常低，交流发电机通过电抗器或欠励磁同步电动机来加载。ZPFC的形状非常类似于开路特性(O.C.C.)，向下和向右移动。
相量图
图1显示了对应于零滞后功率因数负载的交流发电机的相量图。
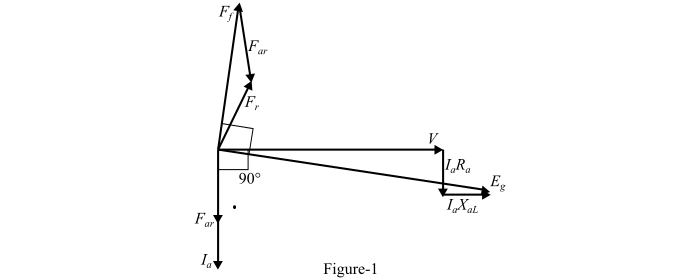
此处，每相端电压(V)作为参考相量。在零滞后功率因数下，电枢电流(𝐼𝑎)滞后于电压V 90°。电枢电阻中的电压降(𝐼𝑎𝑅𝑎)与电流(𝐼𝑎)平行，泄漏电抗中的电压降(𝐼𝑎𝑋𝑎𝐿)垂直于(𝐼𝑎)。
因此，每相产生的电压为：
$$\mathrm{𝐸_{𝑔} = 𝑉 + 𝐼_{𝑎}𝑅_{𝑎} + 𝐼_{𝑎}𝑋_{𝑎L} … (1)}$$
如果
$𝐹_{𝑎𝑟}$ = 电枢反应磁势(与$𝐼_{𝑎}$同相)
$𝐹_{𝑓}$ = 励磁磁势
$𝐹_{𝑟}$ = 气隙中的合成磁势
三个磁势相量𝐹𝑓、𝐹𝑟和𝐹𝑎𝑟同相，其大小由以下等式关联：
$$\mathrm{𝐹_{𝑓} = 𝐹_{𝑟} + 𝐹_{𝑎𝑟} … (2)}$$
如果忽略电枢电阻(𝑅𝑎)，则所得相量图如图2所示。从图2可以看出，每相端电压(V)、电抗电压降(𝐼𝑎𝑋𝑎𝐿)和发电电压(𝐸𝑔)都同相。因此，端电压(V)实际上等于𝐸𝑔和𝐼𝑎𝑋𝑎𝐿的算术差，即：
$$\mathrm{𝑉 = 𝐸_{𝑔} − 𝐼_{𝑎}𝑋_{𝑎𝐿} … (3)}$$
公式(2)和(3)中给出的算术表达式构成了**Potier三角形**的基础。
此外，公式(2)可以通过将两边除以转子上的每极有效匝数(𝑇𝑓)转换为等效励磁电流形式。因此：
$$\mathrm{\frac{𝐹_{𝑓}}{𝑇_{𝑓}}=\frac{𝐹_{r}}{𝑇_{𝑓}}+\frac{𝐹_{𝑎𝑟}}{𝑇_{𝑓}}}$$
$$\mathrm{\Rightarrow\:𝐼_{𝑓} = 𝐼_{𝑟} + 𝐼_{𝑎𝑟} … (4)}$$
Potier三角形
图3显示了O.C.C.和ZPFC。
考虑ZPFC上一点b，对应于额定端电压(V)和励磁电流(𝑂𝑀 = 𝐼𝑓)。
如果在这种运行条件下，电枢反应磁势(𝐹𝑎𝑟)的值以等效励磁电流(𝐿𝑀 = 𝐼𝑎𝑟)表示，则合成磁势(𝐹𝑟)的等效励磁电流为(𝑂𝐿 = 𝐼𝑟)。
此合成励磁电流(𝑂𝐿 = 𝐼𝑟)将根据O.C.C.产生发电电压(𝐿𝑐 = 𝐸𝑔)。由于对于零滞后功率因数运行，发电电压由下式给出：
$$\mathrm{𝑬_{𝑔} = 𝑽 + 𝑰_{𝑎}𝑿_{𝑎𝐿} … (5)}$$
此处，垂直距离ac必须等于泄漏电抗电压降(𝐼𝑎𝑋𝑎𝐿)，其中𝐼𝑎为额定电枢电流。因此，电枢泄漏电抗为：
$$\mathrm{𝑋_{𝑎𝐿} =\frac{每相电压降𝑎𝑐}{额定电枢电流}… (6)}$$
现在，由顶点a、b和c形成的三角形称为**Potier三角形**。
在同步电机中，励磁漏磁通与电枢漏磁通的组合效应产生一个等效泄漏电抗𝑋𝑝，称为**Potier电抗**。它由下式给出：
$$\mathrm{𝑋_{𝑝} =\frac{每相电压降(电压𝑎𝑐)}{零功率因数额定每相电枢电流(𝐼_{𝑎})}… (7)}$$
对于圆柱转子同步电机，Potier电抗(𝑋𝑝)近似等于电枢泄漏电抗(𝑋𝑎𝐿)，而在凸极电机中，𝑋𝑝可能高达𝑋𝑎𝐿的3倍。
4K+ 次浏览
