同步发电机或交流发电机的等效电路和相量图

交流发电机或同步发电机的等效电路如图 1 所示。通过取同步电抗$𝑋_{𝑆} = 𝑋_{𝐴𝑅} + 𝑋_{𝑎}$，交流发电机的等效电路在图 2 中重新绘制。利用等效电路，可以绘制出如下所示的交流发电机的相量图。

参考等效电路，我们可以写出：

$$\mathrm{𝑽 = 𝑬_{𝒂} − 𝑰_{𝒂}(𝑅_{𝒂} + 𝑗𝑋_{𝑆}) … (1)}$$

交流发电机滞后功率因数负载的相量图

交流发电机向滞后功率因数负载供电的相量图如图 3 所示。这里，功率因数为 𝜑 滞后。为了绘制此相量图，将端电压 V 作为参考相量，其方向沿 OA，其中 OA = V。

由于功率因数为 𝜑 滞后，电枢电流 $𝐼_{𝑎}$ 落后于电压 V 一个等于功率因数角 𝜑 的角度，电枢电流相量的方向沿 OB，其中 OB = I_a。电枢电阻 $𝑰_{𝑎}𝑅_{𝑎}$ 电压降由相量 AC 表示，它与电枢电流同相。

同步电抗中的电压降为 $𝑰_{𝑎}𝑋_{𝑆}$，由相量 CD 表示，它超前于电枢电流 I_a 90°，因此相量 CD 的方向垂直于 OB。同步阻抗中的总电压降是 $𝑰_{𝑎}𝑅_{𝑎}$ 和 $𝑰_{𝒂}𝑋_{𝑆}$ 的相量和，由相量 AD 表示。交流发电机中实际产生的电压 E_a 由相量 OD 表示。

可以通过以下方式从三角形 OFD 中确定实际产生的电压 E_a 的大小：

$$\mathrm{𝑂𝐷^{2} = 𝑂𝐹^{2} + 𝐹𝐷^{2} = (𝑂𝐺 + 𝐺𝐹)^{2} + (𝐹𝐶 + 𝐶𝐷)^{2}}$$

$$\mathrm{{𝐸^{2}_{𝑎}} = (𝑉\:cos\:φ + 𝐼_{𝑎}𝑅_{𝑎})^{2} + (𝑉\:sin\:φ + 𝐼_{𝒂}𝑋_{𝑆})^{2}}$$

$$\mathrm{\Rightarrow\:𝐸_{𝑎} = \sqrt{(𝑉\:cos\:φ + 𝐼_{𝑎}𝑅_{𝑎})^{2} + (𝑉\:sin\:φ + 𝐼_{𝒂}𝑋_{𝑆})^{2} … (2)}}$$

交流发电机单位功率因数负载的相量图

交流发电机向单位功率因数负载供电的相量图如图 4 所示。

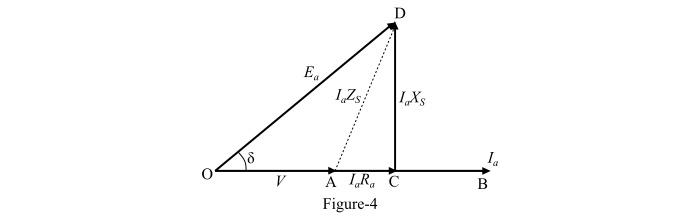
从直角三角形 OCD，可以确定实际产生的电压的大小如下：

$$\mathrm{𝑂𝐷^{2} = 𝑂𝐶^{2} + 𝐶𝐷^{2} = (𝑂𝐴 + 𝐴𝐶)^{2} + (𝐶𝐷)^{2}}$$

$$\mathrm{{𝐸^{2}_{𝑎}} =(𝑉 + 𝐼_{𝑎}𝑅_{𝑎})^{2} + (𝐼_{𝒂}𝑋_{𝑆})^{2}}$$

$$\mathrm{\Rightarrow\:𝐸_{𝑎} = \sqrt{(𝑉 + 𝐼_{𝑎}𝑅_{𝑎})^{2} + (𝐼_{𝒂}𝑋_{𝑆})^{2}}… (3)}$$

交流发电机超前功率因数负载的相量图

交流发电机向超前功率因数负载供电的相量图如图 5 所示。

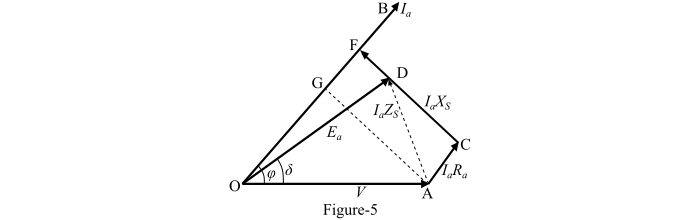
从直角三角形 OFD，可以确定实际产生的电压的大小如下：

$$\mathrm{𝑂𝐷^{2} = 𝑂𝐹^{2} + 𝐹𝐷^{2} = (𝑂𝐺 + 𝐺𝐹)^{2} + (𝐹𝐶 − 𝐶𝐷)^{2}}$$

$$\mathrm{{𝐸^{2}_{𝑎}} =(𝑉\:cos\:φ + 𝐼_{𝑎}𝑅_{𝑎})^{2} + (𝑉\:sin\:φ − (𝐼_{𝒂}𝑋_{𝑆})^{2}}$$

$$\mathrm{\Rightarrow\:𝐸_{𝑎} = \sqrt{(𝑉\:cos\:φ + 𝐼_{𝑎}𝑅_{𝑎})^{2} + (𝑉\:sin\:φ − (𝐼_{𝒂}𝑋_{𝑆})^{2}}… (4)}$$

这里，实际产生的电压 (E_a) 和端电压 (V) 之间的角度称为交流发电机的功率角或转矩角。功率角 (𝛿) 随负载变化，是机器中气隙功率的量度。

Manish Kumar Saini

更新于: 2021年9月30日

15K+ 次查看

启动您的 职业生涯

通过完成课程获得认证

开始学习