同步发电机或交流发电机的功率输入

圆柱转子同步发电机或交流发电机的电路模型如图 1 所示。

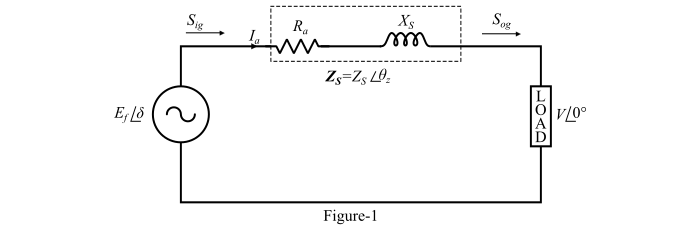
设：

• 𝑉 = 每相端电压

• $𝐸_{𝑓}$ = 每相励磁电压

• $𝐼_{𝑎}$ = 电枢电流

• $\delta$ = 负载角（𝑉 和 $𝐸_{𝑓}$ 之间的夹角）

在电路中应用基尔霍夫电压定律，得到：

$$\mathrm{𝑬_{𝒇} = 𝑽 + 𝑰_{𝒂}𝒁_{𝒔} … (1)}$$

$$\mathrm{∴\:𝑰_{𝒂} =\frac{𝑬_{𝒇} − 𝑽}{𝒁_{𝒔}}… (2)}$$

其中：

$$\mathrm{同步阻抗,\:𝒁_{𝒔} = 𝑅_{𝑎}+ 𝑗𝑋_{𝑎} = 𝑍_{𝑠}\angle 𝜃_{𝑧} … (3)}$$

此外，对于同步发电机，励磁电压 ($𝐸_{𝑓}$) 超前于端电压 (V) 负载角 ($\delta$)。因此，

$$\mathrm{𝑽 = 𝑉 \angle 0°\:\:则\:\:𝑬_{𝒇} = 𝐸_{𝑓} \angle \delta}$$

交流发电机每相复功率输入

交流发电机每相的复功率输入由下式给出：

$$\mathrm{𝑆_{𝑖𝑔} = 𝑃_{𝑖𝑔} + 𝑗𝑄_{𝑖𝑔} =𝑬_{𝒇}{𝑰^{*}_{𝒂}}}$$

$$\mathrm{\Rightarrow\:𝑆_{𝑖𝑔} = 𝑬_{𝒇} \left( \frac{𝑬_{𝒇} − 𝑽}{𝒁_{𝒔}}\right)^{∗}=𝐸_{𝑓}\angle \delta \left(\frac{𝐸_{𝑓}\angle \delta − 𝑉 \angle 0°}{𝑍_{𝑠} \angle 𝜃_{𝑧}} \right)^{∗}}$$

$$\mathrm{\Rightarrow\:𝑆_{𝑖𝑔} = 𝐸_{𝑓}\angle \delta \left(\frac{𝐸_{𝑓}}{𝑍_{𝑠}}\angle(\delta − 𝜃_{𝑧}) − \frac{𝑉}{𝑍_{𝑠}}\angle − 𝜃_{𝑧}\right)^{∗}}$$

$$\mathrm{\Rightarrow\:𝑆_{𝑖𝑔} = 𝐸_{𝑓} \angle \delta \left(\frac{𝐸_{𝑓}}{𝑍_{𝑠}}\angle(𝜃_{𝑧} − \delta) −\frac{𝑉}{𝑍_{𝑠}}\angle 𝜃_{𝑧}\right)}$$

$$\mathrm{\Rightarrow\:𝑆_{𝑖𝑔} = \frac{𝐸^{2}_{𝑓}} {𝑍_{𝑠}}\angle 𝜃_{𝑧} -\frac{𝑉𝐸_{𝑓}}{𝑍_{𝑠}}\angle (𝜃_{𝑧} + \delta)}$$

$$\mathrm{∴\:𝑆_{𝑖𝑔} = 𝑃_{𝑖𝑔} + 𝑗𝑄_{𝑖𝑔}}$$

$$\mathrm{= \frac{𝐸^{2}_{𝑓}}{𝑍_{𝑠}}(cos\:𝜃_{𝑧} + 𝑗\:sin\:𝜃_{𝑧 })}$$

$$\mathrm{− \left[ \frac{𝑉𝐸_{𝑓}}{𝑍_{𝑠}}cos(𝜃_{𝑧} + \delta) + 𝑗\frac{𝑉𝐸_{𝑓}}{𝑍_{𝑠}}sin(𝜃_{𝑧} + \delta)\right]… (4)}$$

$$\mathrm{}$$

交流发电机每相有功功率输入

将式 (4) 的实部相等，得到交流发电机有功功率输入 ($𝑃_{𝑖𝑔}$) 的表达式：

$$\mathrm{𝑃_{𝑖𝑔} =\frac{{𝐸^{2}_{𝑓}} }{𝑍_{𝑠}}cos\:𝜃_{𝑧} −\frac{𝑉𝐸_{𝑓}}{𝑍_{𝑠}}cos(𝜃_{𝑧} + \delta)}$$

从图 2 所示的阻抗三角形，

$$\mathrm{cos\:𝜃_{𝑧} =\frac{𝑅_{𝑎}}{𝑍_{𝑠}}\:\:\:和 \:\:\:𝜃_{𝑧} = 90° − α_{𝑧}}$$

$$\mathrm{∴\:𝑃_{𝑖𝑔} =\frac{𝐸^{2}_{𝑓}}{𝑍^{2}_{𝑠}}𝑅_{𝑎} −\frac{𝑉𝐸_{𝑓}}{𝑍_{𝑠}}cos(90° + \delta − α_{𝑧})}$$

$$\mathrm{∴\:𝑃_{𝑖𝑔} =\frac{𝐸^{2}_{𝑓}}{𝑍^{2}_{𝑠}}𝑅_{𝑎}+\frac{𝑉𝐸_{𝑓}}{𝑍_{𝑠}}sin(\delta − α_{𝑧} ) … (5)}$$

交流发电机每相无功功率输入

将式 (4) 的虚部相等，得到交流发电机无功功率输入 ($𝑄_{𝑖𝑔}$) 的表达式：

$$\mathrm{𝑄_{𝑖𝑔} =\frac{𝐸^{2}_{𝑓}}{𝑍_{𝑠}}sin\:𝜃_{𝑧} −\frac{𝑉𝐸_{𝑓}}{𝑍_{𝑠}}sin(𝜃_{𝑧} + \delta)}$$

从图 2 所示的阻抗三角形，

$$\mathrm{sin\:𝜃_{𝑧} =\frac{𝑋_{𝑠}}{𝑍_{𝑠}}\:\:和\:\:𝜃_{𝑧} = 90° − α_{𝑧}}$$

$$\mathrm{∴\:𝑄_{𝑖𝑔} =\frac{𝐸^{2}_{𝑓}}{𝑍^{2}_{𝑠}}𝑋_{𝑠 }−\frac{𝑉𝐸_{𝑓}}{𝑍_{𝑠}}sin(90° + \delta − α_{𝑧} )}$$

$$\mathrm{\Rightarrow\:𝑄_{𝑖𝑔} =\frac{𝐸^{2}_{𝑓}}{𝑍^{2}_{𝑠}}𝑋_{𝑠 }−\frac{𝑉𝐸_{𝑓}}{𝑍_{𝑠}}cos(\delta − α_{𝑧}) … (6)}$$

注意 – 交流发电机的总机械功率输入为

$$\mathrm{机械功率输入 = 𝑃_{𝑖𝑔} + 旋转损耗}$$

交流发电机每相最大功率输入条件

对于交流发电机的最大功率输入，

$$\mathrm{\frac{𝑑𝑃_{𝑖𝑔}}{𝑑𝛿}= 0\:\:和\:\:\frac{𝑑^{2}𝑃_{𝑖𝑔}}{{𝑑\delta}^{2}} < 0}$$

$$\mathrm{∴\:\frac{𝑑}{𝑑\delta}\left(\frac{𝐸^{2}_{𝑓}}{𝑍^{2}_{𝑠}}𝑅_{𝑎} + \frac{𝑉𝐸_{𝑓}}{𝑍_{𝑠}}sin(\delta − α_{𝑧})\right)= 0}$$

$$\mathrm{0 +\frac{𝑉𝐸_{𝑓}}{𝑍_{𝑠}}cos(\delta − α_{𝑧}) = 0}$$

$$\mathrm{\Rightarrow\:cos(\delta − α_{𝑧}) = 0}$$

$$\mathrm{\Rightarrow\:\delta − α_{𝑧} = 90°}$$

$$\mathrm{\Rightarrow\:\delta = 90° + α_{𝑧} = 90° + (90° − 𝜃_{𝑧} ) = 180° − 𝜃_{𝑧}}$$

因此，对于交流发电机的最大功率输入，

$$\mathrm{负载角(𝛿) = 180° − 阻抗角(𝜃_{𝑧}) … (7)}$$

因此，从式 (5) 和 (7)，交流发电机每相的最大功率输入为

$$\mathrm{𝑃_{𝑖𝑔(𝑚𝑎𝑥)} =\frac{𝐸^{2}_{𝑓}}{𝑍^{2}_{𝑠}}𝑅_{𝑎}+\frac{𝑉𝐸_{𝑓}}{𝑍_{𝑠}}… (8)}$$

Manish Kumar Saini

更新于：2021 年 10 月 18 日

1K+ 次查看

开启您的 职业生涯

完成课程获得认证

开始学习