凸极同步电机（交流发电机）的双反应理论

在凸极转子同步电机中，气隙高度不均匀。考虑一个具有2极凸极转子的同步电机，该转子在2极定子内逆时针旋转，如图1所示。

在图1中，沿转子轴线所示的轴称为直轴或d轴，垂直于d轴的轴称为交轴或q轴。可以看出，d轴磁通($𝜑_{𝑑}$)的路径涉及两个较小的气隙，因此该路径的磁阻最小。q轴磁通($𝜑_{𝑞}$)路径具有两个较大的气隙，它是磁阻最大的路径。

图2显示了垂直向上方向的转子磁场($𝑩_{𝑟}$) 。这个转子磁场在电枢（或定子绕组）中感应电动势。

如果将滞后功率因数负载连接到交流发电机，则将流过电枢电流($𝑰_{𝒂}$) 。电枢电流($𝑰_{𝑎}$)滞后于励磁电压($𝑬_{𝑓}$) ψ角（见图2）。电枢电流($𝑰_{𝑎}$)产生定子磁动势($𝐹_{𝑠}$) ，该磁动势滞后于$𝑰_{𝒂}$ 90°。定子磁动势($𝐹_{𝑠}$)沿$𝐹_{𝑠}$方向产生定子磁场($𝑩_{𝒔}$) 。

根据Blondel的双反应理论，定子磁动势($𝐹_{𝑠}$)可以分解为两个分量，即直轴分量($𝐹_{𝑑}$)和交轴分量($𝐹_{𝑞}$) 。

如果

• $𝜑_{𝑑}$ = 直轴磁通

• $𝜑_{𝑞}$ = 交轴磁通

• $𝑆_{𝑑}$ = 直轴磁通路径的磁阻

• $𝑆_{𝑞}$ = 交轴磁通路径的磁阻

那么，

$$\mathrm{直轴磁通,\:𝜑_{𝑑} =\frac{𝐹_{𝑑}}{𝑆_{𝑑}}… (1)}$$

并且，

$$\mathrm{交轴磁通,\:𝜑_{𝑞} =\frac{𝐹_{𝑞}}{𝑆_{𝑞}}… (2)}$$

由于$𝑆_{𝑑} < 𝑆_{𝑞}$ ，定子磁动势的直轴分量($𝐹_{𝑑}$)产生的磁通比定子磁动势的交轴分量($𝐹_{𝑞}$)产生的磁通多。定子磁通的直轴分量和交轴分量通过电枢反应在定子绕组中产生电压。

设，

• $𝑬_{𝑎𝑑}$ = 电枢反应电压的直轴分量

• $𝑬_{𝑎𝑞}$ = 电枢反应电压的交轴分量

由于每个电枢反应电压与其相应的电枢电流成正比，并且滞后于电枢电流90°，因此电枢反应电压可以写成：

$$\mathrm{𝑬_{𝑎𝑑} = −𝑗𝑰_{𝑑}𝑋_{𝑎𝑑} … (3)}$$

$$\mathrm{𝑬_{𝑎𝑞} = −𝑗𝑰_{𝑞}𝑋_{𝑎𝑞} … (4)}$$

其中，

• $𝑋_{𝑎𝑑}$ 是每相直轴电枢反应电抗。

• $𝑋_{𝑎𝑞}$ 是每相交轴电枢反应电抗。

这里，$𝑋_{𝑎𝑞}$ < $𝑋_{𝑎𝑑}$ ，因为作用在直轴上的给定磁动势所感应的电动势由于其较高的磁阻而小于交轴上的电动势。

现在，电机中感应的合成电动势为：

$$\mathrm{𝑬_{𝑅} = 𝑬_{𝑓} + 𝑬_{𝑎𝑑 }+ 𝑬_{𝑎𝑞}}$$

$$\mathrm{\Rightarrow\:𝑬_{𝑅}=𝑬_{𝑓}-𝑗𝑰_{𝑑}𝑋_{𝑎𝑑}-𝑗𝑰_{𝑞}𝑋_{𝑎𝑞}… (5)}$$

此外，合成电压($𝑬_{𝑅}$)等于端电压与电枢电阻和漏电抗压降的相量和，因此：

$$\mathrm{𝑬_{𝑅}=𝑽 + 𝑰_{𝑎}𝑅_{𝑎} + 𝑗𝑰_{𝑎}𝑋_{𝑙 }… (6)}$$

电枢电流($𝑰_{𝑎}$)被分成两个分量，一个与励磁电压($𝑬_{𝑓}$)同相，另一个与之正交。

如果

• $𝑰_{𝑞}$ = 与$𝑬_{𝑓}$同相的$𝑰_{𝑎}$的交轴分量

• $𝑰_{𝑑}$ = 滞后于$𝑬_{𝑓}$ 90°的$𝑰_{𝑎}$的直轴分量

然后，总电枢电流是$𝑰_{𝑞}$和$𝑰_{𝑑}$的相量和，即：

$$\mathrm{𝑰_{𝑎} = Ｉ_{𝑞} + Ｉ_{𝑑} … (7)}$$

现在，根据公式(5)和(6)，我们得到：

$$\mathrm{𝑬_{𝑓} = 𝑽 + 𝑰_{𝑎}𝑅_{𝑎} + 𝑗𝑰_{𝑎}𝑋_{𝑙} + 𝑗𝑰_{𝑑}𝑋_{𝑎𝑑} + 𝑗𝑰_{𝒒}𝑋_{𝑎𝑞} … (8)}$$

并且，根据公式(7)和(8)，我们得到：

$$\mathrm{𝑬_{𝑓} = 𝑽 + (𝑰_{𝑞} + Ｉ_{𝑑})𝑅_{𝑎} + 𝑗(Ｉ_{𝑞} + Ｉ_{𝑑})𝑋_{𝑙} + 𝑗Ｉ_{𝑑}𝑋_{𝑎𝑑} + 𝑗Ｉ_{𝒒}𝑋_{𝑎𝑞}}$$

$$\mathrm{\Rightarrow\:𝑬_{𝑓 }= 𝑽 + (Ｉ_{𝑞 }+ Ｉ_{𝑑})𝑅_{𝑎} + 𝑗Ｉ_{𝑑}(𝑋_{𝑙} + 𝑋_{𝑎𝑑}) + 𝑗Ｉ_{𝑞} (𝑋_{𝑙} + 𝑋_{𝑎𝑞} )}$$

$$\mathrm{\Rightarrow\: 𝑬_{𝑓 }= 𝑽 + (Ｉ_{𝑞} + Ｉ_{𝑑})𝑅_{𝑎} + 𝑗Ｉ_{𝑑}𝑋_{𝑑 }+ 𝑗Ｉ_{𝑞}𝑋_{𝑞 }… (9)}$$

其中，

$$\mathrm{𝑋_{𝑑} = 𝑋_{𝑙} + 𝑋_{𝑎𝑑}\:\:\:and \:\:\:𝑋_{𝑞} = 𝑋_{𝑙} + 𝑋_{𝑎𝑞}}$$

电抗$𝑋_{𝑑}$称为**直轴同步电抗**，电抗$𝑋_{𝑞}$称为**交轴同步电抗**。

$$\mathrm{∴\:𝑬_{𝑓 }= 𝑽 + Ｉ_{𝑎}𝑅_{𝑎} + 𝑗Ｉ_{𝑑}𝑋_{𝑑} + 𝑗Ｉ_{𝑞}𝑋_{𝑞} … (10)}$$

公式(10)是凸极同步发电机电压方程的最终形式。

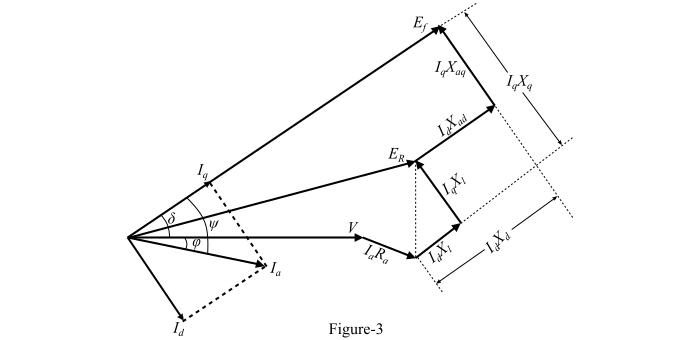
相量图

图3显示了基于Blondel双反应理论的凸极同步发电机的完整相量图。

Manish Kumar Saini

更新于：2021年10月19日

14K+ 浏览量

启动您的职业生涯

完成课程获得认证

开始学习