交流电路中的电阻和阻抗

交流电路中的电阻

考虑包含交流正弦电压源和未知无源元件 (K) 的电路图。只有当元件 K 两端的电压和流经它的电流同相时，元件 K 才为电阻。

解释

设交流电压方程为

$$\mathrm{v=V_{m}\sin\omega\:t\:\:\:...(1)}$$

由于该电压，交流电流 i 将流过元件。现在，所加电压必须克服元件的压降，即

$$\mathrm{v=i\times\:k}$$

$$\mathrm{\Rightarrow\:i=\frac{v}{k}=\frac{V_{m}\sin\omega\:t}{k}\:\:\:...(2)}$$

当sin(ωt) = 1时，电流值最大。

$$\mathrm{\therefore\:I_{m}=\frac{V_{m}}{K}}$$

因此，方程 (2) 变为：

$$\mathrm{i=I_{m}\sin\omega\:t\:\:\:...(3)}$$

从公式 (1) 和 (3) 可以看出，施加的电压和产生的电流同相。因此，未知元件是电阻，即

$$\mathrm{K=R\:\:\:...(4)}$$

交流电路中的阻抗

如果一个交流电路包含电阻和电抗元件，则电路对电流的总阻碍称为交流电路的阻抗。

它用字母“Z”表示，单位为欧姆 (Ω)。

在数学上，阻抗表示为：

$$\mathrm{阻抗,Z=R+jX\:\:\:...(5)}$$

情况 1 – 串联 RL 电路的阻抗

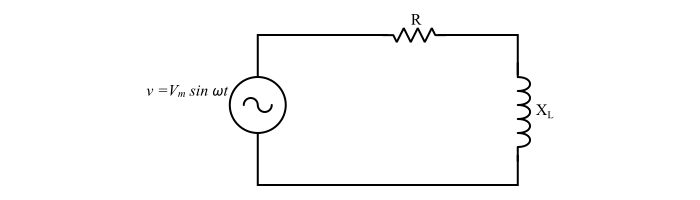
$$\mathrm{Z=R+jX_{L}=R+j\omega\:L\:\:\:...(6)}$$

情况 2 – 串联 RC 电路的阻抗

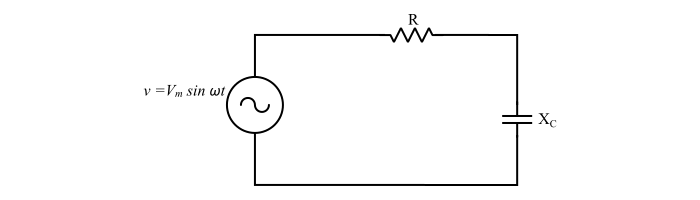
$$\mathrm{Z=R+jX_{C}=R-j\frac{1}{\omega\:C}\:\:\:...(7)}$$

情况 3 – 串联 RLC 电路的阻抗

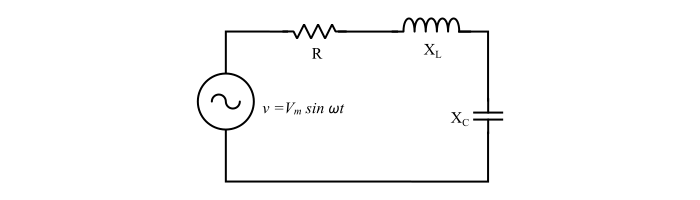
$$\mathrm{Z=R+j(X_{L}-X_{C})=R+j(\omega\:L-\frac{1}{\omega\:C})\:\:\:...(8)}$$

情况 4 – 并联交流电路中的阻抗

对于并联交流电路，阻抗用导纳表示，即

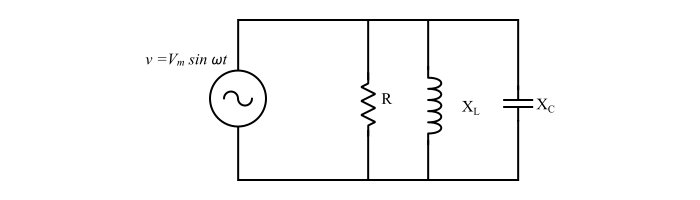
$$\mathrm{阻抗=\frac{1}{导纳}}$$

$$\mathrm{\Rightarrow\:Z=\frac{1}{Y}=\frac{1}{G+jB}\:\:\:....(9)}$$

其中：

• G = 1/R，称为电导

• B = 1/X，称为电纳

Saini Manish Kumar

更新于：2021年7月5日

浏览量 2K+

开启你的职业生涯

完成课程获得认证

开始学习