磁路——串联和并联磁路

磁路

磁路定义为磁通量跟随的闭合路径。

磁路由高导磁率材料制成的芯组成，如铁和软钢等。这是因为这些材料对磁通量的流动阻力很小。

考虑在铁芯上绕有 N 圈的线圈（见图）。当电流 I 流过线圈时，便会形成磁通量 (ψ)。此磁通量遵循闭合路径 ABCDA，因此 ABCDA 为磁路。

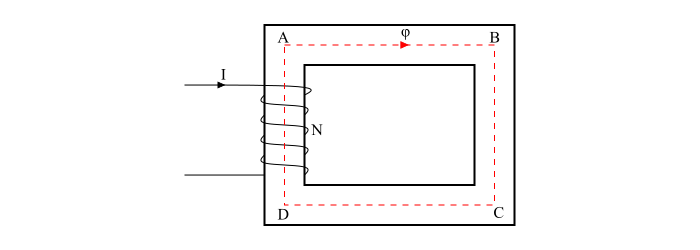
在磁路中，磁芯中的磁通量大小取决于电流 (I)和匝数 (N)。NI 的乘积被称为磁动势 (MMF)。

$$\mathrm{MMF = NI= 安培-匝数}$$

磁路对磁通量流动产生的阻力称为磁路的磁阻 (S)。磁路的磁阻取决于磁路的长度、磁路的横截面积和组成磁路的材料的特性。

磁路类型

磁路有两种类型：

• 串联磁路
• 并联磁路

串联磁路

当相同磁通量 ψ 流过磁路的每个部分时，则该磁路被称为串联磁路。

考虑一个由不同相对磁导率的不同磁性材料组成的复合串联磁路（具有不同尺寸和材料的部分的串联磁路称为复合串联磁路）。该串联磁路的每个部分都将对磁通量 ψ 产生磁阻。由于磁路的不同部分串联，因此总磁阻等于各个部分的磁阻之和。

引用串联磁路的图形，我们有，

$$\mathrm{总磁阻，S_T=\frac{l_1}{\mu_0\mu_r1a_1}+\frac{l_2}{\mu_0\mu_r2a_2}}$$

$$\mathrm{总 MMF = 磁通量 \times 总磁阻}$$

$$\mathrm{\Longrightarrow 总 MMF =\mathit{ψ(\frac{l_1}{\mu_0\mu_r1a_1}+\frac{l_2}{\mu_0\mu_r2a_2}}})}$$

$$\mathrm{\Longrightarrow 总 MMF =\mathit{(\frac{B_1}{\mu_0\mu_r2}})\times l_1+(\frac{B_2}{\mu_0\mu_r2}})\times l_2}}}$$

$$\mathrm{\Longrightarrow 总 MMF = \mathit{H_1\times l_1+H_2\times l_2}}}$$

因此，在串联磁路中建立磁通量所需的总 MMF 是该电路各部分所需 MMF 的总和。

并联磁路

一个有多条磁通量路径的磁路称为并联磁路。

考虑线圈 N 匝绕在线路 AF 上，载有 I 安培的电流。线圈建立的磁通量 $\varphi_1$ 在 B 处分成两条路径 -

• 磁性 $\varphi_2$ 沿着路径 BE 传递。
• 磁通量 $\varphi_3$ 沿着路径 BCDE 传递。

因此，总通量为，

$$\mathrm{\mathit{\varphi_1=\varphi_2+\varphi_3}}}$$

路径 BE 和 BCDE 互为并联，从而形成并联磁路。在并联磁路中，整个并联磁路所需的 MMF 等于任何一条并联路径所需的 MMF。

假设

$$\mathrm{\mathit{S_1} = 磁路 ABEF 的磁阻}$$

$$\mathrm{\mathit{S_2} = 磁路 BE 的磁阻}$$

$$\mathrm{\mathit{S_3} = 磁路 BCDE 的磁阻}$$

因此，

$$\mathrm{总 MMF = 路径 ABEF 的 MMF + 路径 BE 或 BCDE 的 MMF}$$

$$\mathrm{\Longrightarrow 总 MMF = \mathit{\varphi_1S_1+ ψ_2S_2+ \varphi_3S_3}}}$$

马尼什·库马尔·塞尼

更新于： 26-07-2021

16K+ 浏览量

Kickstart Your 职业生涯

完成课程获得认证

开始