数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究串并联电路：定义和示例
一个串并联电路是串联电路和并联电路的组合。在这个电路中，一些元件以串联方式连接，一些以并联方式连接。
在下图所示的电路中，我们可以看到电阻 R2 和 R3 彼此并联连接，并且两者都与 R1 串联连接。
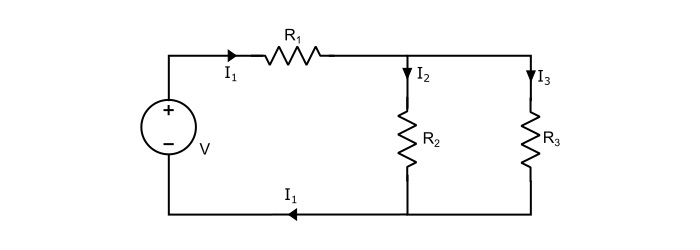
为了解决此类电路，首先将并联支路简化为等效的串联支路，然后将电路作为简单的串联电路求解。
这里，RP 是并联组合的等效电阻，由下式给出：
$$\mathrm{\mathit{R}_{p}=\frac{\mathit{R}_{2}\mathit{R}_{3}}{\mathit{R}_{2}+\mathit{R}_{3}}}$$
总电路电阻 (RT) 由下式给出：
$$\mathrm{\mathit{R}_{r}=\mathit{R}_{1}+\mathit{R}_{p}=\mathit{R}_{1}+\frac{\mathit{R}_{2}\mathit{R}_{3}}{\mathit{R}_{2}+\mathit{R}_{3}}}$$
并联组合上的电压由下式给出：
$$\mathrm{\mathit{V}_{p}=\mathit{I}_{1}\mathit{R}_{p}=\mathit{I}_{1}×\frac{\mathit{R}_{2}\mathit{R}_{3}}{\mathit{R}_{2}+\mathit{R}_{3}}}$$
电路的总功耗等于各个电阻上的功耗之和，如下所示：
$$\mathrm{\mathit{P}_{r}=\mathit{I}_{1}^{2}\mathit{R}_{1}+\mathit{I}_{2}^{2}\mathit{R}_{2}+\mathit{I}_{3}^{2}\mathit{R}_{3}}$$
数值示例
在下图所示的电路中，求未知电阻 R 的值，并确定电路的总电阻和总功耗。已知电压表读数为 10 V。
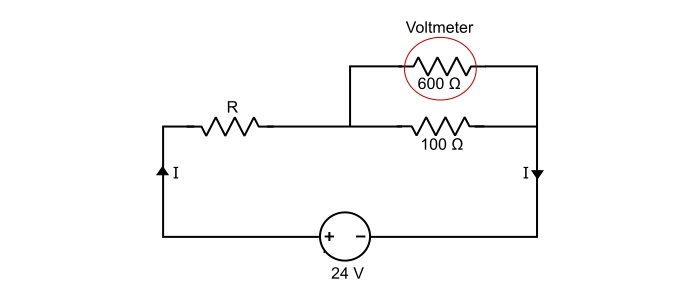
解决方案
参考上图所示电路：
并联组合的总电阻：
$$\mathrm{\mathit{R}_{p}=\frac{600 × 100}{600 + 100}=85.71\:Ω}$$
由于并联组合上的电压等于电压表读数，即 10 V（已知）。因此：
$$\mathrm{电路电流\:\mathit{I}=\frac{10}{85.71}=0.1167\:A}$$
$$\mathrm{R 上的电压\:\mathit{R}=24 − 10 = 14\:V}$$
因此：
$$\mathrm{R 的值\:\:\mathit{R}=\frac{14}{0.1167}=119.96\:Ω}$$
电路的总电阻为：
$$\mathrm{\mathit{R}_{r}=\mathit{R}_{p}+\mathit{R}=119.96 + 85.71 = 205.67\:Ω}$$
电路的总功耗为：
$$\mathrm{\mathit{P}_{r}=\mathit{I}^{2}\mathit{R}_{r}=(0.1167)^{2}× 205.67 = 2.8\:W}$$
5K+ 次查看
