三角傅里叶级数 - 定义和解释

周期信号可以在一定时间间隔内表示为正交函数的线性组合，如果这些正交函数是三角函数，则傅里叶级数表示称为三角傅里叶级数。

解释

考虑一个正弦信号 $x(t)=A\:sin\:\omega_{0}t$，它以时间周期 $T$ 为周期，使得 $T=2\pi/ \omega_{0}$。如果两个正弦波的频率是基频 $(\omega_{0})$ 的整数倍，则这两个正弦波的和也是周期性的。

我们可以证明，一个信号 $x(t)$，它是频率为基频 $(\omega_{0})$ 的整数倍的正弦和余弦函数的和，是一个周期信号。

假设信号 $x(t)$ 由下式给出：

$$\mathrm{x(t)=a_{0}+a_{1}\:cos\:\omega_{0}t+a_{2}\:cos\:2\omega_{0}t+a_{3}\:cos\:3\omega_{0}t+....+a_{k}\:cos\:k\omega_{0}t}$$

$$\mathrm{\:\:\:\:\:\:\:\:\:\:+b_{1}\:sin\:\omega_{0}t+b_{2}\:sin\:2\omega_{0}t+b_{3}\:sin\:3\omega_{0}t+...+b_{k}\:sin\:k\omega_{0}t}$$

$$\mathrm{\Rightarrow\:x(t)=a_{0}+\sum_{n=1}^{k}a_{n}\:cos\:n\omega_{0}t+b_{n}\:sin\:n\omega_{0}t… (1)}$$

其中，$a_{0},a_{1},a_{2}....a_{k}$ 和 $b_{0},b_{1},b_{2}....b_{k}$ 是常数，$\omega_{0}$ 是基频。

同样，如果一个信号 $x(t)$ 是一个周期信号，则它必须满足以下条件：

$$\mathrm{x(t)=x(t+T);\:\:对于所有\:t}$$

因此，

$$\mathrm{\Rightarrow\:x(t+T)=a_{0}+\sum_{n=1}^{k}a_{n}\:cos\:n\omega_{0}(t+T)+b_{n}\:sin\:n\omega_{0}(t+T)}$$

$$\mathrm{\because\:周期,T=\left ( \frac{2\pi}{\omega_{0}}\right )}$$

$$\mathrm{\Rightarrow\:x(t+T)=a_{0}+\sum_{n=1}^{k}a_{n}\:cos\:n\omega_{0}(t+\frac{2\pi}{\omega_{0}})+b_{n}\:sin\:n\omega_{0}(t+\frac{2\pi}{\omega_{0}})}$$

$$\mathrm{\Rightarrow\:x(t+T)=a_{0}+\sum_{n=1}^{k}a_{n}\:cos(n\omega_{0} t+2n\pi)+b_{n}\:sin(n\omega_{0} t+2n\pi)}$$

$$\mathrm{\because\:cos(2n\pi+\theta )=cos\:\theta \:\:和\:\:sin(2n\pi+\theta )=sin\:\theta}$$

使用这些三角恒等式，我们得到：

$$\mathrm{\Rightarrow\:x(t+T)=a_{0}+\sum_{n=1}^{k}a_{n}\:cos(n\omega_{0} t)+b_{n}\:sin(n\omega_{0} t)=x(t)… (2)}$$

从公式 (2) 可以清楚地看出，信号 $x(t)$ 是频率为 0、$\omega_{0}、2\omega_{0}、...k\omega_{0}$ 的正弦和余弦函数的和，是一个周期为 T 的周期信号。如果在 $x(t)$ 的表达式中，$k\rightarrow \infty$，那么我们可以得到任何周期信号 $x(t)$ 的傅里叶级数表示。

因此，任何周期信号都可以表示为正弦和余弦函数的无限和，这些函数本身是角频率为 0、$\omega_{0}、2\omega_{0}、...k\omega_{0}$ 的周期信号。这组谐波相关的正弦和余弦函数在时间间隔 $t$ 到 $(t+T)$ 上形成一组完整的正交函数。

因此，傅里叶级数的三角形式可以定义如下：

频率为 0、$\omega_{0}、2\omega_{0}、...k\omega_{0}$ 的正弦和余弦项的无限级数称为傅里叶级数的三角形式，可以表示为：

$$\mathrm{x(t)=a_{0}+\sum_{n=1}^{\infty}a_{n}\:cos\: n\omega_{0} t+b_{n}\:sin\:n\omega_{0} t… (3)}$$

其中，$a_{0}、a_{n}$ 和 $b_{n}$ 称为三角傅里叶级数系数。

$$\mathrm{a_{0}=\frac{1}{T} \int_{t_{0}}^{(t_{0}+T)}x(t)\:dt… (4)}$$

$$\mathrm{a_{n}=\frac{2}{T} \int_{t_{0}}^{(t_{0}+T)}x(t)\:cos\:n\omega_{0}t\:dt… (5)}$$

$$\mathrm{b_{n}=\frac{2}{T} \int_{t_{0}}^{(t_{0}+T)}x(t)\:sin\:n\omega_{0}t\:dt… (6)}$$

这里，

• 系数 $a_{0}$ 称为直流分量。

• $(a_{1}\:cos\:\omega_{0}t+b_{1}\:sin\:\omega_{0}t)$ 称为基波分量。

• $(a_{2}\:cos\:\omega_{0}t+b_{2}\:sin\:2\omega_{0}t)$称为二次谐波分量。

• 类似地，$(a_{n}\:cos\:n\omega_{0}t+b_{n}\:sin\:n\omega_{0}t)$ 称为n^次谐波分量。

数值示例

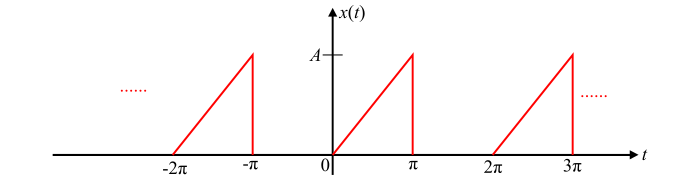
求下图所示波形的三角傅里叶级数。

解答

我们可以看到，给定的波形是周期为 $T= 2\pi$ 的周期信号。

在数学上，给定的波形可以描述为：

$$\mathrm{x(t)=\begin{cases}(\frac{A}{\pi})t & for\:0 ≤ t ≤\:\pi\0 & for\:\pi≤ t ≤2\pi\end{cases}}$$

令，

$$\mathrm{t_{0}=0\:\:和\:\:(t_{0}+T)= 2\pi}$$

然后，给定函数的基频为：

$$\mathrm{\omega_{0}=\frac{2\pi}{T}=\frac{2\pi}{2\pi}=1}$$

因此，系数 $a_{0}$ 由下式给出：

$$\mathrm{a_{0}=\frac{1}{T}\int_{t_{0}}^{(t_{0}+T)}x(t)dt}$$

$$\mathrm{\Rightarrow\:a_{0}=\frac{1}{2\pi}\int_{0}^{2\pi}x(t)\:dt=\frac{1}{2\pi}\int_{0}^{\pi}(\frac{A}{\pi})t\:dt+\frac{1}{2\pi}\int_{0}^{2\pi}0\:dt=\frac{A}{2\pi^{2}}\left [ \frac{t^{2}}{2}\right ]_{0}^{\pi}=\frac{A}{4}}$$

系数 $a_{n}$ 由下式给出：

$$\mathrm{a_{n}=\frac{2}{T} \int_{t_{0}}^{(t_{0}+T)}x(t)cos\:n\omega_{0}t\:\:dt}$$

$$\mathrm{\Rightarrow\:a_{n}=\frac{2}{2\pi} \int_{0}^{\pi}(\frac{A}{\pi})t\:cos\:nt\:dt=\frac{A}{\pi^{2}}\int_{0}^{\pi}t\:cos\:nt\:dt}$$

通过求解上述积分，我们得到：

$$\mathrm{\Rightarrow\:a_{n}=\frac{A}{\pi^{2}n^{2}}[cos\:n\pi]}$$

$$\mathrm{\therefore\:a_{n}=\begin{cases}-(\frac{2A}{\pi^{2}n^{2}}) & for\:n为奇数\0 & for\:n为偶数\end{cases}}$$

类似地，系数 $b_{n}$ 由下式给出：

$$\mathrm{b_{n}=\frac{2}{T}\int_{t_{0}}^{(t_{0}+T)}x(t)sin\:n\omega_{0}t\:dt}$$

$$\mathrm{\Rightarrow\:b_{n}=\frac{2}{2\pi}\int_{0}^{\pi}(\frac{A}{\pi})t\:sin\:nt\:dt=\frac{A}{\pi^{2}}\int_{0}^{\pi}t\:sin\:nt\:dt}$$

求解此积分，我们有：

$$\mathrm{b_{n}=\frac{A}{\pi^{2}}\left [-\frac{\pi\:cos\:n\pi}{n} +\left (\frac{sin\:nt}{n^{2}} \right )_{0}^{\pi} \right ]}$$

$$\mathrm{\Rightarrow\:b_{n}=-\frac{A}{n\pi}cos\:n\pi=\frac{A}{n\pi}(-1)^{n+1}}$$

$$\mathrm{\therefore\:b_{n}=\begin{cases}(\frac{A}{n\pi}) & for\:n为奇数\(-\frac{A}{n\pi}) & for\:n为偶数\end{cases}}$$

因此，三角傅里叶级数为：

$$\mathrm{x(t)=a_{0}+\sum_{n=1}^{\infty}a_{n}\:cos\:n\:\omega_{0}t+b_{n}\:sin\:n\omega_{0}t}$$

$$\mathrm{\Rightarrow\:x(t)=\frac{A}{4}-\frac{2A}{\pi^{2}}\sum_{n=奇数}^{\infty}\frac{cos\:nt}{n^{2}}+\frac{A}{\pi}\sum_{n=1}^{\infty}(-1)^{n+1}\cdot \frac{sin\:nt}{n}}$$

Manish Kumar Saini

更新于: 2021年12月6日

15K+ 次浏览

启动您的 职业生涯

通过完成课程获得认证

开始学习