指数傅里叶级数系数表达式

指数傅里叶级数

周期信号可以在一定的时间区间内表示为正交函数的线性组合。如果这些正交函数是指数函数，则称为指数傅里叶级数。

对于任何周期信号𝑥(𝑡)，指数形式的傅里叶级数表示为：

$$\mathrm{X(t)=\sum_{n=-\infty}^{\infty}C_n e^{jn\omega_0t}\:\:\:...(1)}$$

其中，𝜔₀ = 2𝜋⁄𝑇 是周期函数的角频率。

指数傅里叶级数的系数

为了计算指数级数的系数，我们将公式 (1) 的两边乘以𝑒^{−𝑗𝑚𝜔₀𝑡}，并在一个周期内积分，得到：

$$\mathrm{\int_{t_0}^{t_0+T}x(t)e^{-jm\omega_0t}dt=\int_{t_0}^{t_0+T}(\sum_{n=-\infty}^{\infty}C_ne^{jn\omega_0t})e^{-jm\omega_{0}t}dt}$$

$$\mathrm{\Rightarrow\int_{t_0}^{t_0+T}x(t)e^{-jm\omega_0t}dt=\sum_{n=-\infty}^{\infty}C_n\int_{t_0}^{t_0+T}e^{jn\omega_0t}e^{-jm\omega_0t}dt}$$

$$\mathrm{\because \int_{t_0}^{t_0+T}e^{jn\omega_0t}e^{-jm\omega_0t}dt=\begin{cases}0 & m \ne n \\ T & m = n\end{cases}}$$

$$\mathrm{\therefore \int_{t_0}^{t_0+T} x(t)e^{-jm\omega_0t}dt=TC_m}$$

$$\mathrm{\Rightarrow C_m=\frac{1}{T}\int_{t_0}^{(t_0+T)}x(t)e^{-jm\omega_0t}dt}$$

因此，指数傅里叶级数的傅里叶系数𝐶_𝑛 为：

$$\mathrm{ C_n=\frac{1}{T}\int_{t_0}^{t_0+T}x(t)e^{-jn\omega_0t}dt\:\:\:....(2)}$$

公式 (2) 也称为**分析方程**。

此外，指数傅里叶级数的直流分量𝐶₀ 为：

$$\mathrm{ C_0=\frac{1}{T}\int_{t_0}^{(t_0+T)}x(t)dt\:\:\:....(3)}$$

周期函数 x(t) 的指数傅里叶级数系数只有离散谱，因为系数𝐶𝑛的值仅存在于n的离散值上。由于指数傅里叶级数表示复数谱，因此它具有幅度谱和相位谱。

关于幅度谱和相位谱，需要注意以下几点：

• 幅度线谱始终是n的偶函数。
• 相位线谱始终是n的奇函数。

数值示例

获得图中所示波形的指数傅里叶级数。

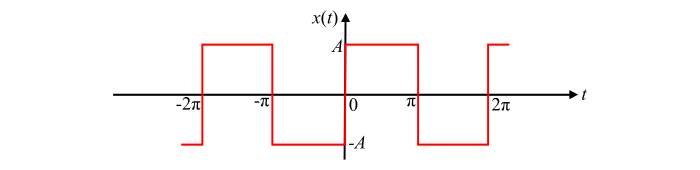
解答

图中所示波形表示周期为 T = 2π 的周期函数，其数学表达式为：

$$\mathrm{x(t)=\begin{cases}A & 0 \leq t\leq \pi\\-A & \pi \leq t\leq 2\pi \end {cases}}$$

$$\mathrm{𝑡_0 = 0 \:and \:(𝑡_0 + 𝑇) = 2\pi}$$

这里，令

因此，该函数的基频为：

$$\mathrm{\omega_0=\frac{2\pi}{T}=\frac{2\pi}{2\pi}=1}$$

现在，指数傅里叶级数系数𝐶₀ 为：

$$\mathrm{C_0=\frac{1}{T}\int_{0}^{T}x(t)dt}$$

$$\mathrm{\Rightarrow C_0=\frac{1}{2\pi}\int_{0}^{\pi}A\:dt+\frac{1}{2\pi}\int_{\pi}^{2\pi}-A\:dt=\frac{A}{2\pi}[(t)^{\pi}_{0}-(t)^{2\pi}_{\pi}]=0}$$

同样，系数𝐶_𝑛 为：

$$\mathrm{C_n=\frac{1}{T} \int_{0}^{T}x(t)e^{-jn\omega_0t}dt}$$

$$\mathrm{\Rightarrow C_n=\frac{1}{2\pi} \int_{0}^{\pi}A\:e^{-jnt}dt+\frac{1}{2\pi} \int_{\pi}^{2\pi}-A\:e^{-jnt}dt}$$

$$\mathrm{\Rightarrow C_n=\frac{A}{2\pi}[(\frac{e^{-jnt}}{-jn})^{\pi}_{0}-(\frac{e^{-jnt}}{-jn})^{2\pi}_{\pi}]}$$

$$\mathrm{\Rightarrow C_n=\frac{-A}{j2n\pi}[(e^{-jnt}-e^{0})-(e^{-j2n\pi}-e^{-jn\pi})]}$$

$$\mathrm{\Rightarrow C_n=\frac{-A}{j2n\pi}[\left \{ (-1)^n-1 \right \}-\left \{ 1-(-1)^n \right \}]=-j\frac{2A}{n\pi}}$$

$$\mathrm{\therefore C_n=\begin{cases}0 & n为偶数 \\ -j\frac{2A}{n\pi} & n为奇数 \end {cases}}$$

因此，给定函数的指数傅里叶级数为：

$$\mathrm{x(t)=\sum_{n=-\infty}^{\infty}C_ne^{jn\omega_0t}=\sum_{n=-\infty}^{\infty}-j\frac{2A}{n\pi}e^{jnt};\:n为奇数}$$

Saini Manish Kumar

更新于：2021年12月6日

13K+ 次浏览

开启您的职业生涯

完成课程获得认证

开始学习