傅里叶余弦级数 – 解释与示例

傅里叶余弦级数是三角傅里叶级数的另一种形式。傅里叶余弦级数也称为极坐标形式傅里叶级数或谐波形式傅里叶级数。

函数 x(t) 的三角傅里叶级数包含相同频率的正弦和余弦项。即：

$$\mathrm{x(t)=a_{0}+\sum_{n=1}^{\infty}a_{n}\:cos\:n\omega_{0} t+b_{n}\:sin\:n\omega_{0} t… (1)}$$

其中：

$$\mathrm{a_{0}=\frac{1}{T}\int_{t_{0}}^{(t_{0}+T)}x(t)\:dt}$$

$$\mathrm{a_{n}=\frac{2}{T}\int_{t_{0}}^{(t_{0}+T)}x(t)\:cos\:n\omega_{0} t\:dt}$$

$$\mathrm{b_{n}=\frac{2}{T}\int_{t_{0}}^{(t_{0}+T)}x(t)\:sin\:n\omega_{0} t\:dt}$$

在公式 (1) 中，将正弦和余弦项的分子和分母乘以 ($\sqrt{a_{n}^{2}+b_{n}^{2}}$)，得到：

$$\mathrm{x(t)=a_{0}+\sum_{n=1}^{\infty}\left( \sqrt{a_{n}^{2}+b_{n}^{2}}\right)\left( \frac{a_{n}}{\sqrt{a_{n}^{2}+b_{n}^{2}}}cos\:n\omega_{0} t+\frac{b_{n}}{\sqrt{a_{n}^{2}+b_{n}^{2}}}sin\:n\omega_{0} t\right)… (2)}$$

将公式 (2) 中的值设为：

$$\mathrm{a_{0}=A_{0}}$$

$$\mathrm{\sqrt{a_{n}^{2}+b_{n}^{2}}=A_{n}… (3)}$$

$$\mathrm{\frac{a_{n}}{\sqrt{a_{n}^{2}+b_{n}^{2}}}=cos\:\theta_{n}\:\:and\:\:\frac{b_{n}}{\sqrt{a_{n}^{2}+b_{n}^{2}}}=-sin\:\theta_{n}}$$

我们得到：

$$\mathrm{x(t)=A_{0}+\sum_{n=1}^{\infty}A_{n}(cos\:\theta_{n}\:cos\:n\omega_{0} t-sin\:\theta_{n}\:sin\:n\omega_{0} t)}$$

$$\mathrm{\Rightarrow\:x(t)=A_{0}+\sum_{n=1}^{\infty}A_{n}\:cos(n\omega_{0} t+\theta_{n})… (4)}$$

其中：

$$\mathrm{\theta_{n}=-tan^{-1} \left(\frac{b_{n}}{a_{n}}\right)… (5)}$$

公式 (4) 中的表达式是函数 x(t) 的余弦表示，它包含频率为 $\omega_{0},2\omega_{0},3\omega_{0},...$ 的正弦曲线。在这个表达式中，$A_{0}$ 称为直流分量，项 $A_{n}[cos(n\omega_{0} t+\theta_{n})]$ 称为函数 x(t) 的第 n 次谐波分量。

这里，$A_{n}$ 表示余弦傅里叶级数的谐波幅度或幅度系数或频谱幅度，而 $\theta_{n}$ 称为余弦傅里叶级数的相位角或相位系数或频谱相位。

数值示例

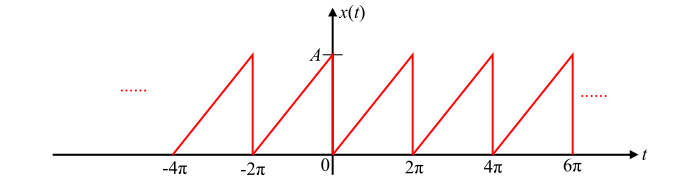
求图中所示波形的余弦傅里叶级数。

解答

图中的波形可以用以下数学表达式描述：

$$\mathrm{x(t)=\frac{A}{2\pi}t;\:\:for\:0 ≤\:t\:≤2\pi}$$

设

$$\mathrm{t_{0}=0\:\:and\:\:(t_{0}+T)=2\pi}$$

因此，给定函数的基频为：

$$\mathrm{\omega_{0}=\frac{2\pi}{T}=\frac{2\pi}{2\pi}=1}$$

现在，可以确定余弦傅里叶级数的系数如下：

$$\mathrm{A_{0}=a_{0}=\frac{1}{T}\int_{t_{0}}^{(t_{0}+T)}x(t)\:dt}$$

$$\mathrm{\Rightarrow\:A_{0}=\frac{1}{2\pi}\int_{0}^{2\pi}\frac{A}{2\pi}t\:dt=\frac{A}{(2\pi)^{2}}\left [\frac{t^{2}}{2} \right ]_{0}^{2\pi}=\frac{A}{(2)}}$$

$$\mathrm{\therefore\:A_{0}=\frac{A}{2}}$$

同样地：

$$\mathrm{a_{n}=\frac{2}{T}\int_{t_{0}}^{(t_{0}+T)}x(t)\:cos\:n\omega_{0} t\:dt}$$

$$\mathrm{\Rightarrow\:a_{n}=\frac{2}{2\pi}\int_{0}^{2\pi}(\frac{A}{2\pi}t)cos\:nt\:dt=\frac{2A}{(2\pi)^{2}}\int_{0}^{2\pi}t\:cos\:nt\:dt}$$

解上述积分，我们得到：

$$\mathrm{a_{n}=\frac{2A}{(2\pi)^{2}}[0]=0}$$

此外：

$$\mathrm{b_{n}=\frac{2}{T}\int_{t_{0}}^{(t_{0}+T)}x(t)sin\:n\omega_{0} t\:dt=\frac{2}{2\pi}\int_{0}^{2\pi}(\frac{A}{2\pi}t)sin\:nt\:dt}$$

$$\mathrm{\Rightarrow\:b_{n}=\frac{2A}{(2\pi)^{2}}\int_{0}^{2\pi}t\:sin\:nt\:dt}$$

解上述积分，我们得到：

$$\mathrm{b_{n}=\frac{2A}{(2\pi)^{2}}(\frac{-2\pi}{n})=\frac{-A}{n\pi}}$$

因此，余弦傅里叶级数的幅度系数为：

$$\mathrm{A_{n}=\sqrt{a_{n}^{2}+b_{n}^{2}}=\sqrt{0+\left(\frac{-A}{n\pi}\right)^{2}}=\frac{A}{n\pi}}$$

余弦傅里叶级数的相位系数为：

$$\mathrm{\theta_{n}=-tan^{-1}\left(\frac{b_{n}}{a_{n}}\right)=-tan^{-1}\left[\frac{\left(\frac{-A}{n\pi}\right)}{0} \right]=-\frac{\pi}{2}}$$

因此，波形的余弦傅里叶级数为：

$$\mathrm{x(t)=A_{0}+\sum_{n=1}^{\infty}A_{n}\:cos(n\omega_{0} t+\theta_{n})}$$

$$\mathrm{\Rightarrow\:x(t)=\frac{A}{2}+\sum_{n=1}^{\infty}\frac{A}{n\pi}cos(nt-\frac{\pi}{2})… (6)}$$

公式 (6) 中的表达式是给定波形的余弦傅里叶级数表示。

Saini Manish Kumar

更新于：2021年12月8日

5K+ 次浏览

开启你的职业生涯

完成课程获得认证

开始学习