数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究正弦和余弦函数的傅里叶变换
傅里叶变换
连续时间函数 $x(t)$ 的傅里叶变换可以定义为：
$$\mathrm{x(\omega)=\int_{−\infty}^{\infty}x(t)e^{-j\omega t }dt}$$
正弦函数的傅里叶变换
令
$$\mathrm{x(t)=sin\:\omega_{0} t}$$
根据欧拉公式，我们有：
$$\mathrm{x(t)=sin\:\omega_{0} t=\left[\frac{ e^{j\omega_{0} t}- e^{-j\omega_{0} t}}{2j} \right]}$$
然后，根据傅里叶变换的定义，我们有：
$$\mathrm{F[sin\:\omega_{0} t]=X(\omega)=\int_{−\infty}^{\infty}x(t)e^{-j\omega t}dt=\int_{−\infty}^{\infty}sin\:\omega_{0}\: t\: e^{-j\omega t}dt}$$
$$\mathrm{ \Rightarrow\:X(\omega)=\int_{−\infty}^{\infty}\left[ \frac{e^{j\omega_{0} t}-e^{-j\omega_{0} t}}{2j}\right] e^{-j\omega t}dt}$$
$$\mathrm{\Rightarrow\:X(\omega)=\frac{1}{2j}\left[ \int_{−\infty}^{\infty}e^{j\omega_{0} t}e^{-j\omega t} dt-\int_{−\infty}^{\infty} e^{-j\omega_{0} t}e^{-j\omega t} dt\right]}$$
$$\mathrm{=\frac{1}{2j}\{F[e^{j\omega_{0} t}] -F[e^{-j\omega_{0} t}]\}}$$
由于复指数函数的傅里叶变换由下式给出：
$$\mathrm{F[e^{j\omega_{0} t}]=2\pi\delta(\omega-\omega_{0})\:\:and\:\:F[e^{-j\omega_{0} t}]=2\pi\delta(\omega+\omega_{0})}$$
$$\mathrm{ \therefore\:X(\omega)=\frac{1}{2j}[2\pi\delta(\omega-\omega_{0})-2\pi\delta(\omega+\omega_{0})]}$$
$$\mathrm{\Rightarrow\:X(\omega)=-j\pi[\delta(\omega-\omega_{0})-\delta(\omega+\omega_{0})]}$$
因此，正弦波的傅里叶变换为：
$$\mathrm{F[sin\:\omega_{0}\:t]=-j\pi[\delta(\omega-\omega_{0})-\delta(\omega+\omega_{0})]}$$
或者，它也可以表示为：
$$\mathrm{sin\:\omega_{0}\:t\overset{FT}{\leftrightarrow}-j\pi[\delta(\omega-\omega_{0})-\delta(\omega+\omega_{0})]}$$
图 1 显示了正弦函数及其幅度和相位谱的图形表示。
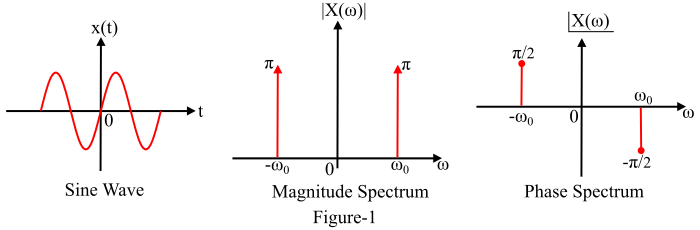
余弦函数的傅里叶变换
给定
$$\mathrm{x(t)=cos\:\omega_{0}t}$$
根据欧拉公式，我们有：
$$\mathrm{cos\:\omega_{0}t=\left[\frac{e^{j\omega_{0} t}+e^{-j\omega_{0} t}}{2}\right]}$$
然后，根据傅里叶变换的定义，我们有：
$$\mathrm{F[cos\:\omega_{0} t]=X(\omega)=\int_{−\infty}^{\infty}x(t)e^{-j\omega t}dt=\int_{−\infty}^{\infty}cos\:\omega_{0} t e^{-j\omega t}dt}$$
$$\mathrm{\Rightarrow\:X(\omega)=\int_{−\infty}^{\infty}\left[\frac{e^{j\omega_{0} t}+e^{-j\omega_{0} t}}{2} \right]e^{-j\omega t}dt}$$
$$\mathrm{\Rightarrow\:X(\omega)=\frac{1}{2}\left[ \int_{−\infty}^{\infty}e^{j\omega_{0} t}e^{-j\omega t} dt+ \int_{−\infty}^{\infty}e^{-j\omega_{0} t}e^{-j\omega t} dt \right]}$$
$$\mathrm{=\frac{1}{2}\{F[e^{j\omega_{0} t}]+ F[e^{-j\omega_{0} t}]\}}$$
$$\mathrm{\Rightarrow\:X(\omega)=\frac{1}{2}[2\pi\delta(\omega-\omega_{0})+2\pi\delta(\omega+\omega_{0})]}$$
$$\mathrm{\Rightarrow\:X(\omega)=\pi[\delta(\omega-\omega_{0})+\delta(\omega+\omega_{0})]}$$
因此，余弦波函数的傅里叶变换为：
$$\mathrm{F[cos\:\omega_{0} t]=\pi[\delta(\omega-\omega_{0})+\delta(\omega+\omega_{0})]}$$
或者，它也可以表示为：
$$\mathrm{cos\:\omega_{0} t\overset{FT}{\leftrightarrow}\pi[\delta(\omega-\omega_{0})+\delta(\omega+\omega_{0})]}$$
图 2 显示了余弦波信号及其幅度和相位谱的图形表示。
98K+ 次查看
