符号函数的傅里叶变换

傅里叶变换

连续时间函数 $x(t)$ 的傅里叶变换可以定义为：

$$\mathrm{X(\omega)=\int_{−\infty}^{\infty}x(t)e^{-j\omega t}dt}$$

符号函数的傅里叶变换

符号函数用 $sgn(t)$ 表示，定义为：

$$\mathrm{sgn(t)=\begin{cases}1 & 当\:t>0\-1 & 当\:t<0 \end{cases}}$$

由于符号函数不是绝对可积的，因此无法直接求出其傅里叶变换。所以，为了求符号函数的傅里叶变换，考虑如下所示的函数。

$$\mathrm{x(t)=e^{-a|t|}sgn(t);\:\:a\rightarrow 0}$$

因此，符号函数可以表示为：

$$\mathrm{x(t)=sgn(t)=\lim_{a\rightarrow \:0}e^{-a|t|}sgn(t)}$$

$$\mathrm{\Rightarrow\:x(t)=\lim_{a\rightarrow \:0}[e^{-at}u(t)-e^{at}u(-t)]}$$

根据傅里叶变换的定义，我们有：

$$\mathrm{X(\omega)=\int_{−\infty}^{\infty}x(t)e^{-j\omega t}\:dt=\int_{−\infty}^{\infty}sgn(t)e^{-j\omega t}\:dt}$$

$$\mathrm{\Rightarrow\:X(\omega)=\int_{−\infty}^{\infty}\left(\lim_{a\rightarrow \:0}[e^{-at}u(t)-e^{at}u(-t)] \right)e^{-j\omega t}\:dt}$$

$$\mathrm{\Rightarrow\:X(\omega)=\lim_{a\rightarrow \:0}\left[\int_{−\infty}^{\infty}e^{-at}e^{-j\omega t}u(t)dt- \int_{−\infty}^{\infty}e^{at}e^{-j\omega t}u(-t)dt\right]}$$

$$\mathrm{\Rightarrow\:X(\omega)=\lim_{a\rightarrow \:0}\left[\int_{0}^{\infty}e^{-(a+j\omega)t}dt- \int_{−\infty}^{0}e^{(a-j\omega)t}dt\right]}$$

$$\mathrm{\Rightarrow\:X(\omega)=\lim_{a\rightarrow \:0}\left[\int_{0}^{\infty}e^{-(a+j\omega)t}dt- \int_{0}^{\infty}e^{-(a-j\omega)t}dt\right]}$$

$$\mathrm{\Rightarrow\:X(\omega)=\lim_{a\rightarrow \:0}\left\{\left[\frac{e^{-(a+j\omega)t}}{-(a+j\omega)}\right]_{0}^{\infty} -\left[\frac{e^{-(a-j\omega)t}}{-(a-j\omega)}\right]_{0}^{\infty}\right \}}$$

$$\mathrm{\Rightarrow\:X(\omega)=\lim_{a\rightarrow \:0}\left\{\left[\frac{e^{-\infty}-e^{0}}{-(a+j\omega)} \right]- \left[\frac{e^{-\infty}-e^{0}}{-(a-j\omega)} \right] \right\}}$$

$$\mathrm{=\lim_{a\rightarrow \:0}\left[ \frac{1}{(a+j\omega)}-\frac{1}{(a-j\omega)}\right]}$$

求解极限，得到：

$$\mathrm{\Rightarrow\:X(\omega)=\frac{1}{j\omega}-\frac{1}{(-j\omega)}=\frac{2}{j\omega}}$$

因此，符号函数的傅里叶变换为：

$$\mathrm{X(\omega)=F[sgn(t)]=\frac{2}{j\omega}}$$

或者，也可以表示为：

$$\mathrm{sgn(t)\overset{FT}{\leftrightarrow}\frac{2}{j\omega}}$$

符号函数傅里叶变换的幅度和相位表示：

$$\mathrm{幅度, |X(\omega)| =\sqrt{0+\left(\frac{2}{\omega}\right)^{2}}=\frac{2}{\omega};\:\:对于所有\:\omega}$$

$$\mathrm{相位,\angle\:X(\omega) =\begin{cases}\frac{\pi}{2}; & 当\:\omega<0 \ -\frac{\pi}{2}; & 当\:\omega>0 \end{cases}}$$

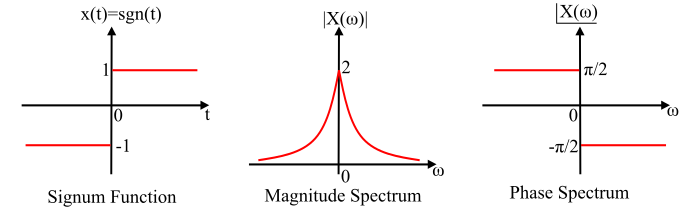
符号函数及其幅度和相位谱的图形表示如下所示。

Manish Kumar Saini

更新于: 2021年12月9日

20K+ 次浏览

开启你的 职业生涯

通过完成课程获得认证

开始学习