数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律学高斯信号的傅里叶变换
对于连续时间函数 $\mathit{x(t)}$，$\mathit{x(t)}$ 的傅里叶变换可以定义为：
$$\mathrm{\mathit{X\left(\omega\right )\mathrm{=}\int_{-\infty }^{\infty} x\left(t\right)\:e^{-j\omega t}\:dt} }$$
高斯信号的傅里叶变换
高斯函数 - 高斯函数定义为：
$$\mathrm{\mathit{g_{a}\left(t\right)\mathrm{=} e^{-at^{\mathrm{2}}} ;\:\:\mathrm{for\:all} \:t} }$$
因此，根据傅里叶变换的定义，我们有：
$$\mathrm{\mathit{X\left(\omega\right)\mathrm{=} F\left [e^{-at^\mathrm{2}} \right ]=\int_{-\infty }^{\infty}e^{-at^\mathrm{2}} \:e^{-j\omega t} \:dt}}$$
$$\mathrm{\Rightarrow \mathit{X\left(\omega\right) \mathrm{=}\int_{-\infty}^{\infty} e^{-\left(at^\mathrm{2}+j\omega t\right) }\:dt \mathrm{=}e^{-\left(\omega^\mathrm{2}/\mathrm{4}a\right)}\int_{-\infty}^{\infty}e^{\left [{-t\sqrt{a}+(j\omega/\mathrm{2}\sqrt{a})}\right]^{2}}}dt }$$
令：
$$\mathrm{\mathit{\left [t\sqrt{a}+(j\omega /\mathrm{2}\sqrt{a})\right ]\mathrm{=} u}}$$
则：
$$\mathrm{\mathit{du\mathrm{=} \sqrt{a} \:dt\:\mathrm{and}\: \:dt\mathrm{=} \frac{du}{\sqrt{a}}}}$$
$$\mathrm{\mathit{\therefore X\left(\omega\right)\mathrm{=}e^{-\left(\omega^\mathrm{2}/\mathrm{4}a\right)}\int_{-\infty }^{\infty} \frac{e^{-u^{\mathrm{2}}}}{\sqrt{a}}\:du\:\mathrm{=} \frac{e^{-\left(\omega^\mathrm{2}/\mathrm{4}a\right)}}{\sqrt{a}}\int_{-\infty }^{\infty}e^{-u^{\mathrm{2}}} \:du}}$$
$$\mathrm{\mathit{\because\int_{-\infty }^{\infty}e^{-u^{\mathrm{2}}} \:du\mathrm{=} \sqrt{\pi}}}$$
$$\mathrm{\mathit{\therefore X\left(\omega\right)\mathrm{=}\frac{e^{-\left(\omega^\mathrm{2}/\mathrm{4}a\right)}}{\sqrt{a}}\cdot \sqrt{\pi}\mathrm{=} \sqrt{\frac{\pi}{a}} \cdot e^{-\left(\omega^\mathrm{2}/\mathrm{4}a\right)} } }$$
因此，高斯函数的傅里叶变换为：
$$\mathrm{\mathit{F\left [e^{-at^{\mathrm{2}}}\right ] \mathrm{=}\sqrt{\frac{\pi}{a}} \cdot e^{-\left ( \omega^\mathrm{2}/\mathrm{4}a\right )}} }$$
或者，它也可以写成：
$$\mathrm{\mathit{e^{-at^\mathrm{2}}\overset{FT}{\leftrightarrow} \sqrt{\frac{\pi}{a}} \cdot e^{-\left (\omega^\mathrm{2}/\mathrm{4}a\right )}}}$$
高斯函数及其频谱的图形表示如图 1 所示。
高斯调制函数的傅里叶变换
高斯调制信号 定义为
$$\mathrm{\mathit{x\left(t \right)\mathit{=} e^{-at^{\mathrm{2}}}\:\mathrm{cos} \:\omega _{\mathrm{0}}t}}$$
$$\mathrm{\mathit{\Rightarrow x\left(t \right)\mathit{=} e^{-at^{\mathrm{2}}} \left (\frac{e^{j\omega _{\mathrm{0}}t}\mathrm{+}e^{-j\omega _{\mathrm{0}}t}}{\mathrm{2}}\right);\left\{\because \mathrm{cos}\:\omega _{\mathrm{0}}t\mathit{=}\left (\frac{e^{j\omega _{\mathrm{0}}t}\mathrm{+}e^{-j\omega _{\mathrm{0}}t}}{\mathrm{2}}\right) \right \}}}$$
因此，高斯调制信号的傅里叶变换为
$$\mathrm{\mathit{X\left( \omega\right) \mathrm{=} \mathrm{\frac{1}{2}}F\left [ e^{-at^{\mathrm{2}}}e^{j\omega _{0}t} \right ] \mathrm{+} }\mathrm{\frac{1}{2}}F\left [ e^{-at^{\mathrm{2}}}e^{-j\omega _{0}t} \right ]}$$
利用傅里叶变换的频移特性 [即 $\mathit{e^{-j\omega _{\mathrm{0}}t}x\left (t\right)\overset{FT}{\leftrightarrow}X \left(\omega\mathrm{+} \omega_{\mathrm{0}}\right)}]$，得到：
$$\mathrm{\mathit{F\left[e^{-at^{\mathrm{2}}}e^{j\omega _{0}t} \right]}\mathrm{\mathrm{=}F\left [e^{-at^{\mathrm{2}}} \right]|_{\omega \mathrm{=}\left ( \omega-\omega _{\mathrm{0}}\right )} }}$$
和
$$\mathrm{\mathit{F\left[e^{-at^{\mathrm{2}}}e^{-j\omega _{0}t} \right]}\mathrm{\mathrm{=}F\left [e^{-at^{\mathrm{2}}} \right]|_{\omega \mathrm{=}\left ( \omega\mathrm{+}\omega _{\mathrm{0}}\right )} }}$$
此外，高斯函数的傅里叶变换为：
$$\mathrm{\mathit{F\left [e^{-at^{\mathrm{2}}}\right ] \mathrm{=}\sqrt{\frac{\pi}{a}} \cdot e^{-\left ( \omega^\mathrm{2}/\mathrm{4}a\right )}}}$$
因此，高斯调制函数的傅里叶变换为：
$$\mathrm{X\left( \omega\right) \mathrm{=}\mathrm{\frac{1}{2}\left[\mathit{\sqrt{\frac{\pi}{a}} \cdot e^{-\left [\left(\omega-\omega _{\mathrm{0}}\right)^{\mathrm{2}}/\mathrm{4}a\right]} \mathrm{+} }\sqrt{\frac{\pi}{a}} \cdot e^{-\left [\left(\omega \mathrm{+}\omega _{\mathrm{0}}\right)^{\mathrm{2}}/\mathrm{4}a\right]}\right ]}}$$
或者，它也可以表示为：
$$\mathrm{\mathit{e^{-at^{\mathrm{2}}}\:\mathrm{cos} \:\omega _{\mathrm{0}}t}\overset{FT}{\leftrightarrow}\mathrm{\frac{1}{2}\left[\mathit{\sqrt{\frac{\pi}{a}} \cdot e^{-\left [\left(\omega-\omega _{\mathrm{0}}\right)^{\mathrm{2}}/\mathrm{4}a\right]} \mathrm{+} }\sqrt{\frac{\pi}{a}} \cdot e^{-\left [\left(\omega \mathrm{+}\omega _{\mathrm{0}}\right)^{\mathrm{2}}/\mathrm{4}a\right]}\right ]}}$$
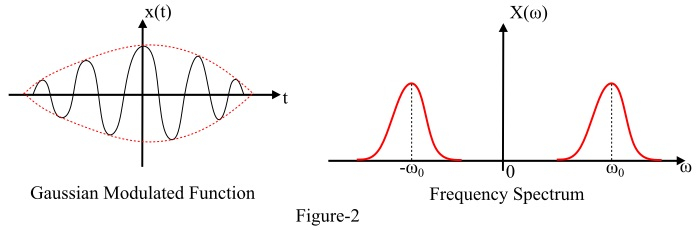
高斯调制信号及其频谱的图形表示如图 2 所示。
16K+ 浏览量
