数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学单位阶跃函数的傅里叶变换
傅里叶变换
对于连续时间函数$x(t)$，傅里叶变换定义为：
$$\mathrm{X(\omega)=\int_{−\infty }^{\infty}x(t)e^{−j\omega t}\:dt}$$
单位阶跃函数的傅里叶变换
单位阶跃函数定义为：
$$\mathrm{u(t)=\begin{cases}1 & t≥ 0\0 & t< 0\end{cases}}$$
由于单位阶跃函数不是绝对可积的，因此无法直接求出其傅里叶变换。
为了求出单位阶跃函数的傅里叶变换，我们将单位阶跃函数表示为符号函数的形式：
$$\mathrm{u(t)=\frac{1}{2}+\frac{1}{2}sgn(t)=\frac{1}{2}[1+sgn(t)]}$$
已知
$$\mathrm{x(t)=u(t)=\frac{1}{2}[1+sgn(t)]}$$
现在，根据傅里叶变换的定义，我们有：
$$\mathrm{F[u(t)]=X(\omega)=\int_{−\infty }^{\infty}x(t)e^{-j\omega t} dt=\int_{−\infty }^{\infty} u(t)e^{-j\omega t} dt}$$
$$\mathrm{\Rightarrow\:X(\omega)=\int_{−\infty }^{\infty} \frac{1}{2}[1+sgn(t)]e^{-j\omega t}dt}$$
$$\mathrm{\Rightarrow\:X(\omega)=\frac{1}{2}\left [ \int_{−\infty }^{\infty} 1 \cdot e^{-j\omega t} dt + \int_{−\infty }^{\infty} sgn(t) \cdot e^{-j\omega t} dt\right ]}$$
$$\mathrm{\Rightarrow\:X(\omega)=\frac{1}{2}\{ F[1]+ F[sgn(t)]\}}$$
常数幅度和符号函数的傅里叶变换为：
$$\mathrm{F[1]=2\pi\delta(\omega)\:\:and\:\:F[sgn(t)]=\frac{2}{j\omega}}$$
$$\mathrm{\therefore\:F[u(t)]=X(\omega)=\frac{1}{2}\left [2\pi\delta(\omega) + \frac{2}{j\omega}\right ] }$$
因此，单位阶跃函数的傅里叶变换为：
$$\mathrm{F[u(t)]=\left (\pi\delta(\omega) + \frac{1}{j\omega}\right )}$$
或者，它也可以表示为：
$$\mathrm{u(t)\overset{FT}{\leftrightarrow}\left ( \pi\delta(\omega) +\frac{1}{j\omega}\right )}$$
单位阶跃函数傅里叶变换的幅度和相位表示：
$$\mathrm{幅度,|X(\omega)|=\begin{cases}∞ & \omega = 0\0 & \omega= −\infty & \omega= \infty\end{cases}}$$
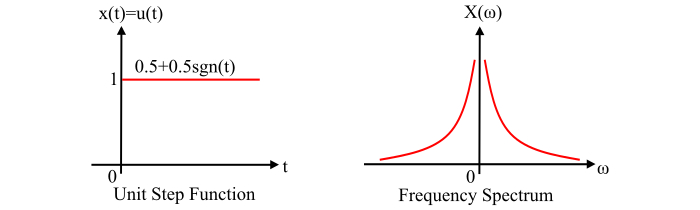
单位阶跃函数及其频谱的图形表示如图所示。
47K+ 浏览量
