如何计算等效电阻（串联和并联电路示例）

---

在电气和电子电路中，电阻被定义为导体材料对电流（或电荷）流动产生的摩擦量。用于在电路中引入电阻的电路元件称为电阻器。电阻器是一种无源电路元件，它控制着电流通过电路的流动，并将多余的电能转化为热能。有时，我们需要的电路中所需的电阻值没有现成的电阻器。因此，我们会以特定的方式将两个或多个电阻器连接起来，以获得电路中所需的电阻值。

在本教程中，我们将了解等效电阻是什么，以及当电阻器串联或并联或串并联连接时，如何确定它们的等效电阻。我们还将讨论三种组合的数值示例，以便更好地理解这个概念。

如何在串联电路中计算等效电阻？

一种电阻器组合方式，其中电阻器首尾相连，形成链状，并且只提供一条电流路径，称为电阻器的串联连接，或简称为串联电阻。

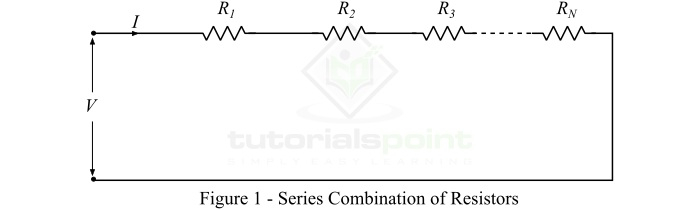
为了理解串联等效电阻的计算，考虑N个电阻，分别为R₁、R₂、R₃……R_N，串联连接，如图1所示。假设组合的总电压为V伏特，I为组合的总电流。需要注意的是，电流I对所有电阻器都是相同的。

根据欧姆定律，我们有：

$$\mathrm{V_{1}=IR_{1};\: V_{2}=IR_{2};\: \cdot \cdot \cdot V_{N}=IR_{N}}$$

此外，

$$\mathrm{V=V_{1}+V_{2}+V_{3}+\cdot \cdot \cdot + V_{N}}$$

$$\mathrm{\Rightarrow V=IR_{1}+IR_{2}+IR_{3}+\cdot \cdot \cdot + IR_{N}}$$

$$\mathrm{\Rightarrow V=I\left ( R_{1}+R_{2}+R_{3}+\cdot \cdot \cdot + R_{N} \right )}$$

但是，

$$\mathrm{\frac{V}{I}=R_{eq}}$$

因此，

$$\mathrm{R_{eq}=R_{1}+R_{2}+R_{3}+\cdot \cdot \cdot +R_{N}}$$

因此，当多个电阻器串联连接时，串联组合的等效电阻可以通过简单地将所有电阻值相加来计算。

特殊情况 - 当N个相同电阻值（例如R）的电阻器串联连接时，它们的等效电阻由以下公式计算：

$$\mathrm{R_{eq}=N\times R}$$

其中，N是串联组合的电阻器总数。

以下是关于电阻器串联组合的一些重要要点，您应该注意：

• 串联组合的等效电阻等于所有电阻之和。

• 串联电阻组合的等效电阻始终大于组合中最大的电阻。

• 通过串联所有电阻的电流相同。

• 每个电阻上的压降不同，取决于电阻值。

• 电阻器串联连接是为了将电压分成多个较小的电压值。

如何在并联电路中计算等效电阻？

一种电阻器组合方式，其中所有电阻器的一端连接到一个公共点，另一端连接到另一个公共点，使得电阻器数量和电流路径数量相等，称为电阻器的并联组合。

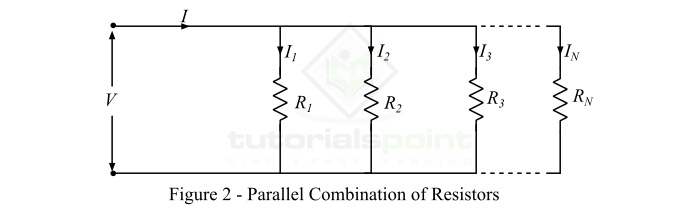
现在，为了理解并联电阻组合的等效电阻计算过程，考虑N个电阻并联连接，如图2所示。从图2可以看出，所有电阻器上的电压相同，都等于V伏特，但每个电阻器上的电流不同，取决于电阻值。

根据欧姆定律，

$$\mathrm{I_{1}=\frac{V}{R_{1}};\:I_{2}=\frac{V}{R_{2}};\: I_{3}=\frac{V}{R_{3}};\: \cdot \cdot \cdot I_{N}=\frac{V}{R_{N}} }$$

此外，

$$\mathrm{I=I_{1}+I_{2}+I_{3}+ \cdot \cdot \cdot +I_{N}}$$

$$\mathrm{\Rightarrow I=\frac{V}{R_{1}}+\frac{V}{R_{2}}+\frac{V}{R_{3}}+ \cdot \cdot \cdot +\frac{V}{R_{N}}}$$

$$\mathrm{\Rightarrow I=V\left ( \frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}}+ \cdot \cdot \cdot +\frac{1}{R_{N}} \right )}$$

但是，

$$\mathrm{\frac{I}{V}=\frac{1}{R_{eq}}}$$

因此，

$$\mathrm{\frac{1}{R_{eq}}=\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}}+ \cdot \cdot \cdot +\frac{1}{R_{N}}}$$

因此，当多个电阻并联连接时，组合的等效电阻的倒数等于各个电阻倒数之和。

当只有两个电阻并联连接时，等效电阻由以下公式给出：

$$\mathrm{\frac{1}{R_{eq}}=\frac{1}{R_{1}}+\frac{1}{R_{2}}=\frac{R_{1}+R_{2}}{R_{1}R_{2}}}$$

$$\mathrm{\therefore R_{eq}=\frac{R_{1}R_{2}}{R_{1}+R_{2}}}$$

因此，当两个电阻并联连接时，组合的等效电阻等于两个电阻的乘积除以它们的和。

特殊情况 - 当所有N个并联连接的电阻器具有相同的电阻值（例如R）时，组合的等效电阻由以下公式给出：

$$\mathrm{ R_{eq}=\frac{R}{N}}$$

以下是关于电阻器并联组合的一些重要要点：

• 并联电阻组合的等效电阻小于组合中最小的电阻。

• 通过每个电阻的电流不同。

• 所有电阻器上的电压相同。

• 并联电阻组合充当分流器，因为它将单个电流分成多个电流。

串并联电阻组合的等效电阻

有时，我们会遇到一些电路，其中一些电阻器串联连接，另一些电阻器并联连接。这种电阻器组合通常被称为串并联电阻组合。图3显示了一个电阻网络，其中电阻器以串并联方式连接。

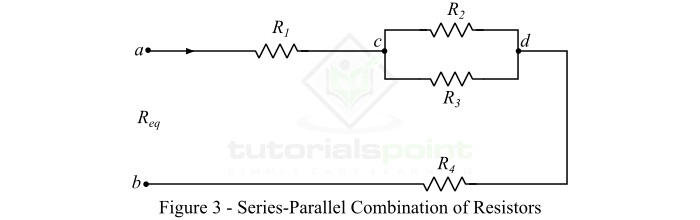
串并联电阻组合的等效电阻可以通过以下两个步骤计算：

步骤1

计算所有并联连接电阻器的等效电阻。对于给定的示例，我们有：

$$\mathrm{ R_{cd}=\frac{R_{2}R_{3}}{R_{2}+R_{3}}}$$

步骤2

计算串联连接电阻器的等效电阻。因此，对于给定的示例，我们有：

$$\mathrm{ R_{eq}=R_{1}+R_{cd}+R_{4}}$$

或者

$$\mathrm{ R_{eq}=R_{1}+\left ( \frac{R_{2}R_{3}}{R_{2}+R_{3}} \right )+R_{4}}$$

数值示例（1）

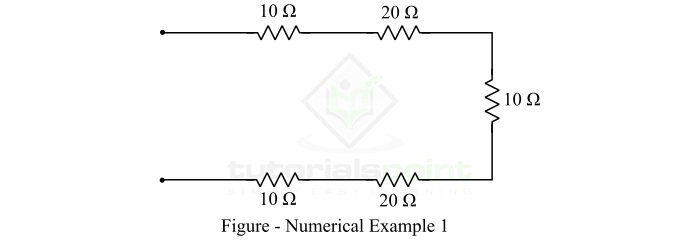
计算以下电阻网络的等效电阻：

解决方案

可以观察到，在给定的网络中，电阻器是串联组合的。因此，它们的等效电阻将为：

$$\mathrm{ R_{eq}=10 + 20 + 10 + 20 + 10}$$

$$\mathrm{ R_{eq}=70\: \Omega }$$

数值示例（2）

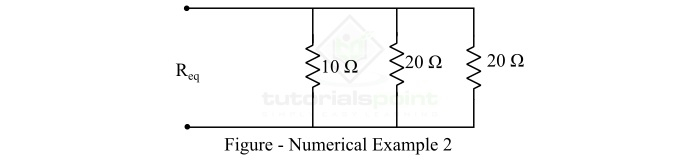
计算以下电阻网络的等效电阻：

解决方案

通过观察，可以清楚地看出网络中的电阻器是并联排列的。因此，组合的等效电阻将为：

$$\mathrm{\frac{1}{R_{eq}} =\frac{1}{10}+\frac{1}{20}+\frac{1}{20} }$$

$$\mathrm{\frac{1}{R_{eq}} =\frac{2 + 1 + 1}{20}+=\frac{4}{20}}$$

$$\mathrm{\therefore R_{eq} =5 \: \Omega } $$

数值示例（3）

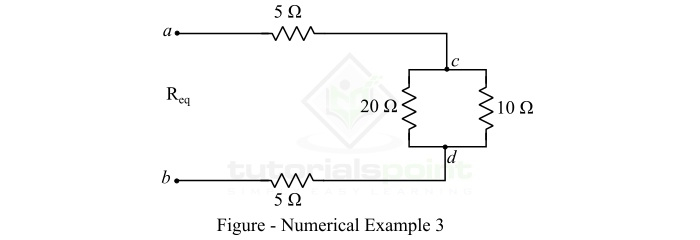
计算以下电阻网络的等效电阻。

解决方案

我们可以看到，该网络有一些电阻器串联连接，也有一些电阻器并联连接。

10欧姆和20欧姆并联电阻的等效电阻为：

$$\mathrm{ R_{cd} =\frac{10\times 20}{10+20} } $$

$$\mathrm{\Rightarrow R_{cd} =\frac{ 200}{30}=6.67\, \Omega }$$

现在，所有电阻器都串联连接。因此，网络的等效电阻为：

$$\mathrm{ R_{eq} =5 + 6.67 + 5=16.67\, \Omega } $$

结论

在本教程中，我们讨论了电阻器集合可以以三种方式组合：串联、并联和串并联。在串联组合中，组合的等效电阻等于所有电阻之和。在并联组合中，组合的等效电阻的倒数等于各个电阻倒数之和。

根据电路的要求或为了在电路中引入所需的电阻值，当没有特定电阻值的单个电阻器可用时，电阻器会以串联或并联的方式组合。