确定串联和并联电阻的等效电阻

---

介绍

电路是这里最重要的因素，它在电阻并联连接时起作用。可以看出，并联电路中每个电阻的电位差保持相同，但电流在电阻中的流动并不相同。总电流的计算是通过将每个电阻器中的电流相加来完成的。

并联电路的应用已在家庭配电中得到体现。这种电路更适合应用于避免短路，并有助于监控不同设备的电流流动。

目的

这两个因素的主要目的是确定这些电阻在并联连接时的等效电阻。

理论

可以看出，当两个或两个以上的电阻连接在两点之间时，这种情况称为并联连接。在并联情况下，各电阻两端的电位差保持相同（Brainigniter，2022）。这方面另一个重要的方面是，流过电阻的电流看起来是不同的。公式显示为

$$\mathrm{1/R_p = 1/R_1 \:+\: 1/R_2 \:+\: 1/R_3}$$

所需材料

此因素的检查需要不同的材料。在所需材料中，有：两个电阻、电流表、电池消除器、所需的插头钥匙、一块砂纸、连接线、电阻箱和电压表（Betrained，2022）。这些被认为是检查过程中的重要材料。

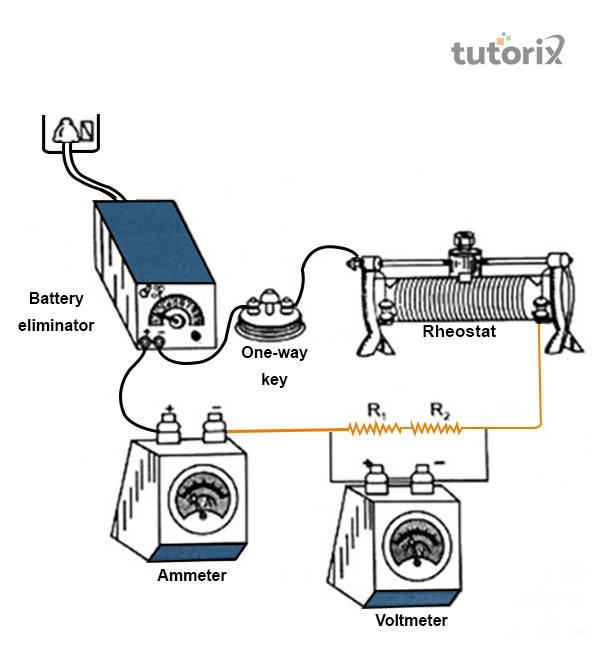
图1：孔径排列

电路图和步骤

首先，需要根据电路图(i)设置设备。之后，需要插入钥匙并调节电阻箱。调整将持续进行，直到电压表和电流表显示读数，这是通过滑动变量来完成的（Yang *等*，2019）。

然后读取电流表和电压表的读数，然后关闭电池一段时间。在接下来的图中，重复这些步骤。使用公式R = V/1计算电阻。这是计算图中电阻的步骤。

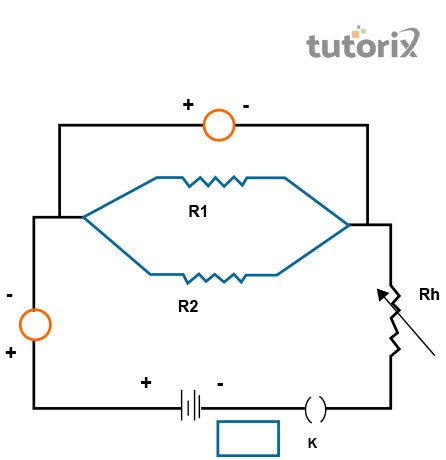
图2：电路图

观察表

$\mathrm{R_1}$ 表格

序号	电压表读数 (V)	电流表读数 (I)	电阻 (R = V/I)
1.	0.02 V	0.01 A	2 $\mathrm{\Omega}$
2.	0.04 V	0.02 A	保持不变
3.	0.08 V	0.04 A	保持不变

表1：$\mathrm{R_1}$ 值计算

这里，$\mathrm{R_1}$ 的平均值为 $\mathrm{(2+2+2)/3 = 2\:\Omega}$

$\mathrm{R_2}$ 表格

序号	电压表读数 (V)	电流表读数 (I)	电阻 (R = V/I)
1.	0.01 V	0.01 A	1 $\mathrm{\Omega}$
2.	0.02 V	0.02 A	1 $\mathrm{\Omega}$
3.	0.04 V	0.04 A	1 $\mathrm{\Omega}$

表2：$\mathrm{R_2}$ 值计算

这里，$\mathrm{R_2}$ 的平均值为 $\mathrm{(1+1+1)/3 = 1\:\Omega}$

$\mathrm{R_p}$ 表格

序号	电压表读数 (V)	电流表读数 (I)	电阻 (R = V/I)
1.	0.02 V	0.03 A	2/3 $\mathrm{\Omega}$
2.	0.04 V	0.06 A	2/3 $\mathrm{\Omega}$
3.	0.06 V	0.09 A	2/3 $\mathrm{\Omega}$

表3：$\mathrm{R_3}$ 值计算

这里，$\mathrm{R_p}$ 的平均值为 $\mathrm{(2/3+2/3+2/3)/3 = 2/3\:\Omega = 0.67\:\Omega}$

结果

此事的结果是，计算出的等效电阻值 $\mathrm{(R_p)=2/3\:\Omega\:=\:0.67\:\Omega}$ 该值来自等效电阻的实验 $\mathrm{(R_p)=2/3\:\Omega\:=\:0.67\:\Omega}$ Ω（电子学，2022）。这里最重要的因素是 $\mathrm{R_p}$ 小于各个电阻。

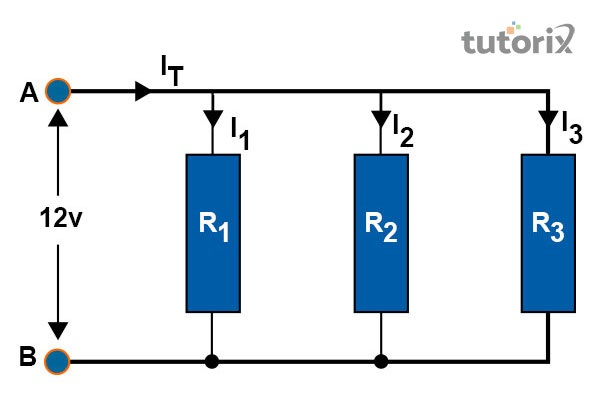
图3：并联电阻

注意事项

此过程需要在该问题中采取一些预防措施。它指出，粗铜线应该比连接线更有效。在这种情况下，所有导线的连接都必须牢固（Helseth，2019）。重要的是要注意电压表的连接，并且连接应该与电阻并联。电流的流动应该持续很短时间，以避免电路不必要的加热。

结论

这里的想法是并联电路和串联电路的概念。这里电压表以并联方式连接，并且当电阻串联时进行连接。在这种情况下，可以使用合成电阻获得最大结果。这里最重要的点是电阻应该串联连接。电压表的连接器指出连接应该根据实验设置的设置进行。

常见问题解答 (FAQs)

Q1. 串联电路中等效电阻的概念是什么？

答：可以看出，等效电阻是电阻的代数和。欧姆定律有助于找到电路中的电流流动。它等于电压，并且除以等效电阻。

Q2. 两个串联连接的电阻的等效概念是什么？

答：可以看出，当两个相等的电阻串联连接时，串联的总电阻将为 R + R = 2R。串联的概念通过上面给出的公式来描述。

Q3. 为什么并联和串联的电阻不同？

答：该概念彼此不同，因为并联电路具有不同的特性。还可以看出，总电阻也与电阻之和不同。