并联电阻

当每个电阻的一端连接到一个公共点，而每个电阻的另一端连接到另一个公共点，使得电流流动的路径数与电阻数相同，则称为并联电路。

下图显示了三个电阻并联连接到直流电压源 V 的情况。设电路电流为 𝐼，支路电流分别为 I₁、I₂ 和 I₃。每条支路的电压降相同，因此根据欧姆定律，我们可以写成：

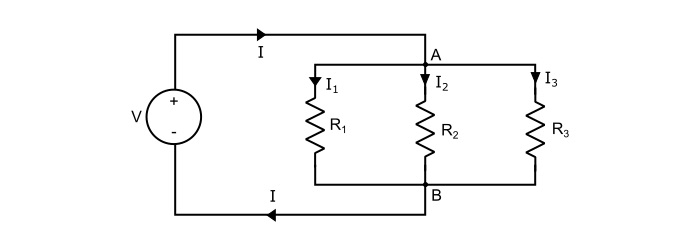
$$\mathrm{\mathit{V}=\mathit{I}_{1}\mathit{R}_{1}=\mathit{I}_{2}\mathit{R}_{2}=\mathit{I}_{3}\mathit{R}_{3}}$$

此外，参考电路：

$$\mathrm{\mathit{I}=\mathit{I}_{1}+\mathit{I}_{2}+\mathit{I}_{3}}$$

$$\mathrm{\Rightarrow\frac{\mathit{V}}{\mathit{R}_{p}}=\frac{\mathit{V}}{\mathit{R}_{1}}+\frac{\mathit{V}}{\mathit{R}_{2}}+\frac{\mathit{V}}{\mathit{R}_{3}}}$$

其中，R_P 是三个电阻并联的等效电阻。因此，

$$\mathrm{\frac{1}{\mathit{R}_{p}}=\frac{1}{\mathit{R}_{1}}+\frac{1}{\mathit{R}_{2}}+\frac{1}{\mathit{R}_{3}}}$$

上述电路中的功率损耗由下式给出：

$$\mathrm{\mathit{P}_{p}=(\frac{\mathit{V}^{2}}{\mathit{R}_{1}}+\frac{\mathit{V}^{2}}{\mathit{R}_{2}}+\frac{\mathit{V}^{2}}{\mathit{R}_{3}})=(\mathit{I}_{1}^2\mathit{R}_{1}+\mathit{I}_{2}^2\mathit{R}_{2}+\mathit{I}_{3}^2\mathit{R}_{3})}$$

因此，电路的总功率损耗是各个电阻功率损耗的总和，即：

$$\mathrm{\Rightarrow \mathit{P}_{p}=\mathit{P}_{1}+\mathit{P}_{2}+\mathit{P}_{3}}$$

两个电阻并联

这里，两条支路电路的等效电阻为

$$\mathrm{\frac{1}{\mathit{R}_{eq}}=\frac{1}{\mathit{R}_{1}}+\frac{1}{\mathit{R}_{2}}}$$

$$\mathrm{\Rightarrow\:\mathit{R}_{eq}=\frac{\mathit{R}_{1}\mathit{R}_{2}}{\mathit{R}_{1}+\mathit{R}_{2}}=\frac{两个电阻的乘积}{两个电阻的和}}$$

因此，在两个电阻的并联电路中，等效电阻的值等于两个电阻的乘积除以它们的和。

此外，对于两条支路电路，

$$\mathrm{\mathit{V}=\mathit{I}_{1}\mathit{R}_{1}=\mathit{I}_{2}\mathit{R}_{2}}$$

并且，

$$\mathrm{\mathit{I}=\mathit{I}_{1}+\mathit{I}_{2}=\mathit{V}(\frac{1}{\mathit{R}_{1}}+\frac{1}{\mathit{R}_{2}})=\mathit{I}_{1}(\frac{\mathit{R}_{1}+\mathit{R}_{2}}{\mathit{R}_{2}})=\mathit{I}_{2}(\frac{\mathit{R}_{1}+\mathit{R}_{2}}{\mathit{R}_{1}})}$$

因此，

$$\mathrm{\mathit{I}_{1}=\mathit{I}(\frac{\mathit{R}_{2}}{\mathit{R}_{1}+\mathit{R}_{2}})}$$

同样地，

$$\mathrm{\mathit{I}_{2}=\mathit{I}(\frac{\mathit{R}_{1}}{\mathit{R}_{1}+R_{2}})}$$

因此，在两个电阻的并联电路中，一个电阻中的电流等于总电流乘以与其相反的电阻再除以两个电阻的和。

数值示例 - 1

求下图所示电路的等效电阻。已知，R₁ = R₄ = 10 Ω 和 R₂ = RR₃ = 5 Ω。

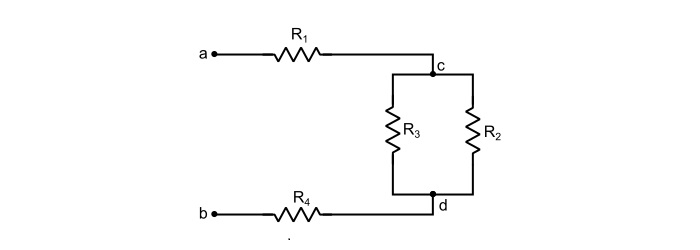
解决方案

已知，R1 = R4 = 10 Ω 和 R2 = R3 = 5 Ω，则

参考问题中所示的电路，我们可以写成：

$$\mathrm{\Rightarrow\:\mathit{R}_{cd}=\frac{\mathit{R}_{2}\mathit{R}_{3}}{\mathit{R}_{2}+\mathit{R}_{3}}=\frac{5×5}{5+5}=2.5 Ω}$$

$$\mathrm{\Rightarrow\:\mathit{R}_{ab}=\mathit{R}_{1}+\mathit{R}_{cd}+\mathit{R}_{4}=10+2.5+10=22.5 Ω}$$

因此，a 和 b 端子之间的等效电阻等于 22.5 Ω。

数值示例 - 2

在下图所示的电路中，确定x-y 端子之间的等效电阻。

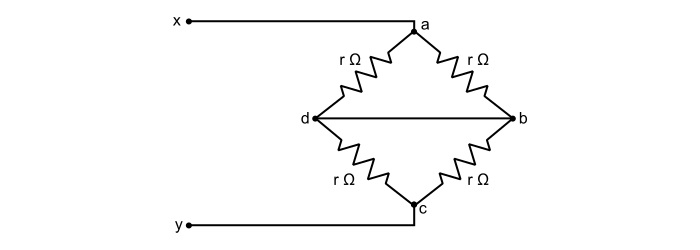
解决方案

重新排列电路为：

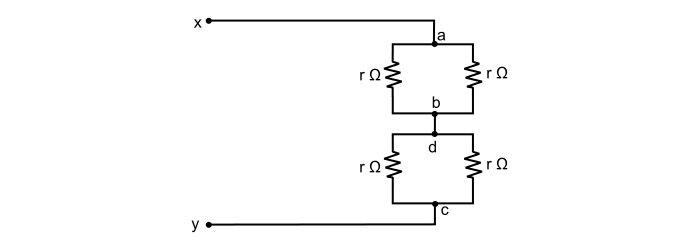
这里，

$$\mathrm{\mathit{R}_{ab}=\frac{r}{2}\:\:\:and\:\:\:\mathit{R}_{cd}=\frac{r}{2}}$$

$$\mathrm{\Rightarrow\:\mathit{R}_{xy}=\mathit{R}_{ab}+\mathit{R}_{cd}=\frac{r}{2}+\frac{r}{2}=r\:Ω}$$

数值示例 - 3

求电路的等效电阻。

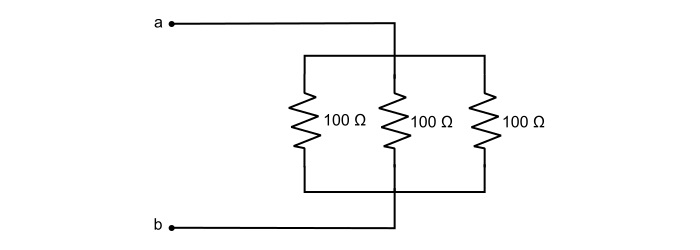
解决方案

参考电路，

$$\mathrm{\frac{1}{\mathit{R}_{ab}}=\frac{1}{100}+\frac{1}{100}+\frac{1}{100}=\frac{3}{100}}$$

$$\mathrm{\Rightarrow\:\mathit{R}_{ab}=\frac{3}{100}=33.33 Ω}$$

Manish Kumar Saini

更新于: 2021年6月18日

259 次查看

开启您的 职业生涯

通过完成课程获得认证

开始学习