交流电路中的电阻

---

重要术语

• 交流电路 − 交流电流所遵循的闭合路径称为交流电路。

• 电阻 − 材料在电流路径中提供的阻碍程度称为该材料的电阻。具有电阻的元件称为电阻器。

• 电压或电流峰值 − 交流量达到的最大值。也称为幅度。

• 平均值 − 一个周期内所有交流量值的算术平均值称为平均值。对于正弦电压或电流，

$$\mathrm{I_{avg}=\frac{2I_{m}}{\pi}=0.637I_{m}}$$

$$\mathrm{V_{avg}=\frac{2V_{m}}{\pi}=0.637I_{m}}$$

• 均方根 (RMS) 值 − 交流电流的RMS值是指在给定时间内流过给定电阻时产生与交流电流在相同电阻和相同时间内产生的热量相同的直流电流值。正弦电流和电压的RMS值是：

$$\mathrm{I_{RMS}=\frac{I_{m}}{\sqrt{2}}=0.707I_{m}}$$

$$\mathrm{V_{RMS}=\frac{V_{m}}{\sqrt{2}}=0.707V_{m}}$$

• 瞬时功率 (p) − 它是电阻上的瞬时电压(v)与流过电阻的瞬时电流(i)的乘积。

瞬时功率值可能是正值或负值。正值表示功率从电源流向负载。负值表示功率从负载流向电源。

$$\mathrm{瞬时功率\:(p)=\upsilon i=\frac{V_{m}I_{m}}{2}-\frac{V_{m}I_{m}}{2}cos(2 \omega t)\:\:\:(瓦)}$$

• 平均功率 (P) − 平均功率是一个周期内瞬时功率的平均值。

$\mathrm{平均功率\:(p)= (p=}$
$\upsilon i)在一个周期内的平均值=\frac{V_{m}I_{m}}{2}=VI\:\:(瓦)$

$$\mathrm{V=施加电压的RMS值}$$

$$\mathrm{I=电路电流的RMS值}$$

包含电阻的交流电路

考虑一个电路，其中包含一个纯电阻R Ω 欧姆，连接到交流电压源。

设交流电压由以下方程给出：

$$\mathrm{ u=V_{m}sin\:\omega t} ...(1)$$

由于该电压，交流电流i将流过电路。整个施加电压仅出现在电阻两端。因此，

$$\mathrm{ u=iR}$$

$$\mathrm{i=\frac{ u}{R}=\frac {v_{m}\:sin\:\omega t }{R}=I_{m}\:sin\:\omega t.....(2)}$$

$$其中，\mathrm{I_{m}=\frac{V_{m}}{R}=电路电流的最大值}$$

从公式(1)和(2)可以看出，流过纯电阻的电流与电阻两端的电压同相。

Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.

电阻电路中的功率

• 瞬时功率

$$\mathrm{p= u i=\frac{V_{m}I_{m}}{2}-\frac{V_{m}I_{m}}{2}cos(2 \omega t)}$$

瞬时功率由两部分组成，即一个常数部分 (V_mI_m/2) 和一个波动部分 (V_mI_m/2)cos 2ωt。

• 平均功率

$$\mathrm{平均功率\:(p)= (p=}$ $\upsilon i)在一个周期内的平均值=\frac{V_{m}I_{m}}{2}=VI}$$

相量图和波形图

• 相量图

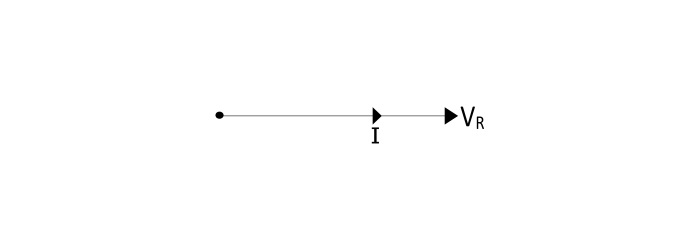
• 电流和电压波形图

• 功率曲线

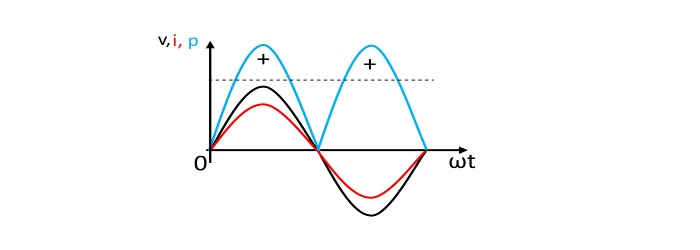
数值例子

一个交流电路包含一个20Ω的纯电阻，并连接到一个240V、50Hz的交流电源。计算(i)电路电流 (ii)电阻消耗的功率和 (iii)电压和电流的方程。

解答

• 电路电流

$$\mathrm{I=\frac{V}{R}=\frac{240}{20}=12A}$$

• 电路消耗的功率

$$\mathrm{P=VI=240×12=2880\:W}$$

• 电压和电流的方程

$$\mathrm{V_{m}=\sqrt{2}V=\sqrt{2}×240=339.36\:V}$$

$$\mathrm{I_{m}=\sqrt{2}I=\sqrt{2}×12=16.97 A}$$

$$\mathrm{\omega=2\pi f=2\pi×50=314\:rad/sec}$$

因此，

$$\mathrm{ u=339.36sin(314t)\:\:\:V}$$

$$\mathrm{i=16.97sin(314t)\:\:\:A}$$