直流电路中的电容器

电容器与电容

当两个导电表面被绝缘材料隔开时，就被称为电容器。导电表面称为电容器的极板，绝缘材料称为介电质。

电容器储存电荷的能力称为电容器的电容。用 C 表示，单位为法拉（F）。

通过实验发现，储存在电容器中的电荷 (Q) 与其两端的电位差成正比，即：

$$Q\varpropto\:V$$

$$\Rightarrow\:Q=CV$$

$$\Rightarrow\:C=\frac{Q}{V}\:\:\:\:...(1)$$

其中，C 是一个常数，称为电容器的电容。

因此，电容器的电容 (C) 定义为电容器任一极板上的电荷 (Q) 与其两端电位差 (V) 的比值。

电容的单位是

$$\because\:C=\frac{Q}{V}$$

$$\therefore\:C 的单位=\frac{库仑}{伏特}=法拉$$

电容器是如何储存电荷的？

考虑一个并联板电容器通过开关连接到 V 伏特的电池上。电容器的充电过程可以理解如下：

步骤 1 - 开关 S 打开时，电容器的极板上没有电荷。

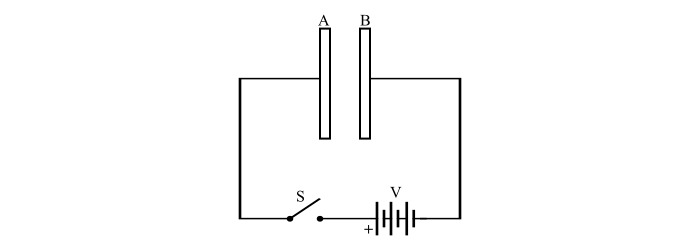
步骤 2 - 当开关 S 闭合时，电池的正极吸引极板 A 上的电子，并将这些电子积累到极板 B 上。这导致极板 A 变得越来越正，极板 B 变得越来越负。此动作称为电容器的充电。电容器的充电过程持续到电容器两端的电位差等于电池电压 (V) 时。

步骤 3 - 一旦电容器充满到电池电压 (V)，电流就会停止流动。

步骤 4 - 现在，如果打开开关 S，电容器的极板将保持电荷。因此，此时，据说电容器已充电。

重要事项

关于电容器的作用，需要注意以下几点：

• 当在电容器两端施加直流电压时，充电电流将持续流动，直到电容器完全充电时电流停止。此充电过程将在非常短的时间内发生，即几分之一秒。因此，完全充电的电容器会阻挡直流电流的流动。

• 只有电子通过外部电路从一个极板转移到另一个极板。电流不会在电容器的极板之间流动。

• 当电容器充电时，两个极板带有相等且相反的电荷。因此，电容器上的电荷是指任一极板上的电荷。

• 为电容器充电所需的能量由外部电源提供。

电容器在直流电路中的行为

可以从以下几点了解电容器在直流电路中的行为：

• 当在未充电的电容器两端施加直流电压时，电容器会快速（不是瞬间）充电到施加的电压。充电电流由下式给出：

$$i=\frac{dQ}{dt}=\frac{d(CV)}{dt}=C\frac{dV}{dt}\:\:\:\:(2)$$

• 当电容器完全充电时，电容器两端的电压变得恒定，并且等于施加的电压。因此，(dV/dt = 0)，因此，充电电流为零。

• 未充电电容器两端的电压为零，因此就直流电压而言，它等效于短路。

• 当电容器完全充电时，电路中没有电流流动。因此，完全充电的电容器对直流电表现为开路。

电容器的充电

考虑一个电容为 C 的未充电电容器，通过一个串联电阻 R 连接到 V 伏特的电池（直流电）上，以将充电电流限制在安全范围内。当开关 S 闭合时，充电电流流过电路，电容器开始充电。

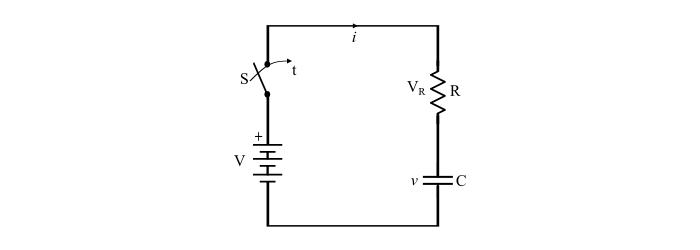
充电电流在开关闭合的瞬间最大，随着电容器两端的电压增加而逐渐减小。当电容器完全充电到施加电压 (V) 时，充电电流降至零。

开关闭合的瞬间

开关闭合的瞬间，电容器两端的电压为零（因为电容器开始时未充电）。整个电压 V 出现在电阻 R 两端，充电电流最大。因此，

$$初始充电电流，I_{m}=\frac{V}{R}$$

$$电容器两端的电压，v=0$$

$$电容器上的电荷，Q=0$$

在任意时间点 t

闭合开关后，充电电流开始减小，电容器两端的电压逐渐增大。因此，在任意时间点 t，

$$电容器两端的电压=v$$

$$电容器上的电荷，q=Cv$$

$$充电电流，i=C\frac{dv}{dt}$$

电容器两端的电压 -

通过在电路中应用 KCL，我们可以写出：

$$V=V_{R}+v$$

$$\Rightarrow\:V=iR+v=(C\frac{dv}{dt})R+v\:\:\:\:\:...(3)$$

$$\Rightarrow\:\frac{dv}{V-v}=\frac{dt}{RC}$$

对两边进行积分：

$$\int\frac{dv}{V-v}=\int\frac{dt}{RC}$$

求解此积分，我们得到：

$$-\log_{e}{(V-v)}=\frac{t}{RC}+K\:\:\:\:...(4)$$

K 的值可以由初始条件确定。在闭合开关的瞬间，t = 0 且 v = 0。因此，从公式 (4) 中，

$$-\log_{e}{V}=K$$

将 K 的值代入方程 (4)，我们得到：

$$-\log_{e}{(V-v)}=\frac{t}{RC}-\log_{e}{(V)}$$

$$\Rightarrow\:\log_{e}{(V-v)}-\log_{e}{(V)}=-\frac{t}{RC}$$

$$\Rightarrow\:\log_{e}{(\frac{V-v}{V})}=-\frac{t}{RC}$$

对两边取反对数，我们得到：

$$\frac{V-v}{V}=e^{-t/RC}$$

$$\Rightarrow\:V-v=Ve^{-t/RC}\:\:\:\:...(5)$$

$$\Rightarrow\:v=V(1-e^{-t/RC})\:\:\:\:...(6)$$

公式 (5) 显示，在充电过程中，电容器两端的电压呈指数增长。

充电电流 -

从公式 (3) 中，

$$V-v=iR$$

从公式 (5) 中，

$$V-v=Ve^{-t/RC}$$

$$\therefore\:iR=Ve^{-t/RC}$$

$$\Rightarrow\:i=\frac{V}{R}e^{-t/RC}=I_{m}e^{-t/RC}\:\:\:\:...(7)$$

其中，I_m 是初始充电电流。此外，从公式 (7) 可以看出，充电电流呈指数下降。充电电压和充电电流的方程也可以用图形表示，如下所示。

时间常数 -

时间常数可以定义为电容器电压 (v) 上升到其最终稳定值 V 所需的时间。用 Tau (τ) 表示，由下式给出：

$$时间常数，\tau=RC\:秒\:\:\:\:...(8)$$

电容器的放电

考虑一个电容为 C 法拉的已充电电容器，通过开关 S 与电阻 R 串联连接。当开关打开时，电容器两端的电压为 V 伏特。当开关闭合时，放电电流开始流过电路，电容器开始放电，即其两端的电压开始下降。放电电流瞬间上升到 Im 值，然后降至零。

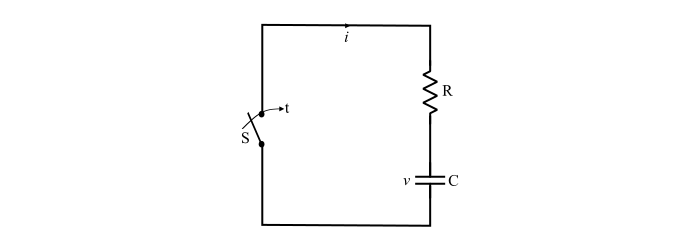
放电电压 -

考虑在放电过程中的任意时间点 t，

$$电容器两端的电压=v$$

$$放电电流，i=C\frac{dV}{dt}$$

通过在电路中应用 KVL，我们得到：

$$V+iR=0$$

$$\Rightarrow\:v+CR\frac{dV}{cdt}=0$$

$$\Rightarrow\:\frac{dV}{v}=-\frac{dt}{RC}$$

对两边积分，我们得到：

$$\log_{e}{v}=-\frac{t}{RC}+K\:\:\:\:...(9)$$

K 的值可以由初始条件确定。在闭合开关的瞬间，t = 0 且 v = V。因此，从公式 (9) 中，

$$\log_{e}{V}=K$$

因此，公式 (9) 变为：

$$\log_{e}{v}=-\frac{t}{RC}+\log_{e}{V}$$

$$\Rightarrow\log_{e}{\frac{v}{V}}=-\frac{t}{RC}$$

对两边取反对数，我们得到：

$${\frac{v}{V}}=e^{-t/RC}$$

$$\Rightarrow\:v=Ve^{-t/RC}\:\:\:\:...(10)$$

公式 (10) 显示，在电容器放电过程中，其两端的电压呈指数下降。

放电电流

放电电流的方向与充电电流的方向相反，即

$$i=-I_{m}e^{-t/RC}\:\:\:...(11)$$

放电电压和放电电流的方程也可以用图形表示，如下所示。

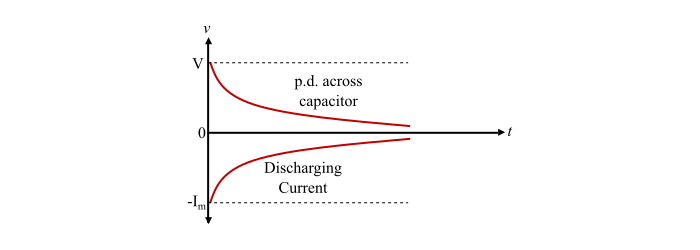
数值示例

一个4 μF的电容器通过1 MΩ的电阻连接到120伏的直流电源。

确定以下内容 -

• 时间常数

• 初始充电电流

• 开关闭合后5秒电容器两端的电压

• 电容器完全充电所需的时间。

解答 -

• 时间常数

$$\tau=RC=(1\times\:10^{6})\times\:(4\times\:10^{-6})=4\:秒$$

• 初始充电电流

$$I_{m}=\frac{V}{R}=\frac{120}{1\times\:10^{6}}=120μ\:A$$

• 开关闭合后5秒电容器两端的电压

$$\because\:v=V(1-e^{-t/RC})=120\times\:(1-e^{-5/4})=85.62V$$

• 电容器完全充电所需的时间

电容器完全充电所需的时间 = 5 × 时间常数

$$\therefore\:t_{full\:charged}=5\times\:4=20\:秒$$

Manish Kumar Saini

更新于: 2021年7月2日

13K+ 次查看

开启您的 职业生涯

通过完成课程获得认证

开始学习