如何计算不同类型电容器的电容？

---

电容 - 定义

电容器存储电荷的能力称为其电容。换句话说，电容也可以定义为材料的一种特性，由于它阻碍了施加在其上的电压的任何变化。

电容：公式

实验发现，存储在电容器中的电荷Q与其两端的电压成正比，即

$$Q\propto\:V$$

$$Q=CV$$

其中，C为常数，称为电容器的电容。

$$\Rightarrow\:C=\frac{Q}{V}$$

因此，电容器的电容(C)也可以定义为任一极板上的电荷与其两端电压之比。

Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.

电容单位

我们已经看到，

$$C=\frac{Q}{V}=\frac{库仑}{伏特}=法拉$$

电容的SI单位是库仑/伏特，也称为法拉，用F表示。

等效电容

情况1 - 当电容器串联连接时

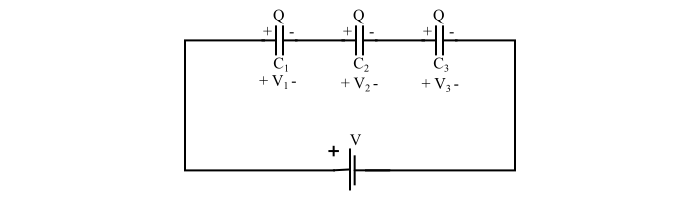
参考电路图，我们可以写出：

$$V=V_{1}+V_{2}+V_{3}=(\frac{Q}{C_{1}}+\frac{Q}{C_{2}}+\frac{Q}{C_{3}})=Q(\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}})$$

$$\Rightarrow\:\frac{V}{Q}=(\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}})$$

$$\Rightarrow\frac{1}{C_{r}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}$$

根据此公式，可以确定串联连接电容器的总等效电容。

情况2 - 当电容器并联连接时

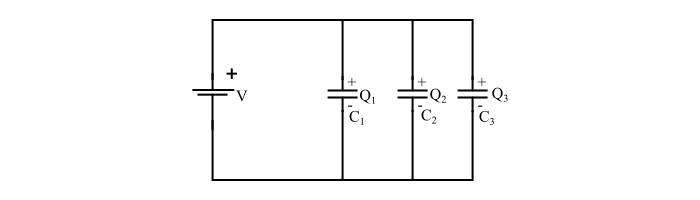
参考电路图，可以写出：

$$Q=Q_{1}+Q_{2}+Q_{3}=C_{1}V+C_{2}V+C_{3}V=V(C_{1}+C_{2}+C_{3})$$

$$\Rightarrow\:\frac{Q}{V}=(C_{1}+C_{2}+C_{3})$$

$$\Rightarrow\:C_{r}=C_{1}+C_{2}+C_{3}$$

以上公式给出了并联连接电容器的总电容。

平行板电容器的电容

情况1 - 具有均匀介质

考虑一个平行板电容器，它由两个面积为A的极板组成。两极板之间的距离为d。两极板之间存在空气作为介质。

因此，平行板电容器的电容为：

• 与每个极板的表面积(A)成正比。

• 与极板之间的距离(d)成反比。

因此，

$$电容，C\propto\:\frac{A}{d}$$

$$\Rightarrow\:C=\varepsilon_{0}\frac{A}{d}$$

其中，ε₀为比例常数，称为真空或空气的绝对介电常数，其值为8.854 × 10^{−12 F/m 。}

如果在电容器的极板之间放置均匀的介质材料，则电容器的电容变为：

$$C=\varepsilon_{0}\varepsilon_{r}\frac{A}{d}$$

其中，ε_r  为介质材料的相对介电常数。

情况2 - 具有复合介质

假设电容器极板之间的空间被三种厚度分别为d₁、d₂和d₃，相对介电常数分别为ε_r1、ε_r2和ε_r3的介质材料占据。则各个部分的电容为：

$$C_{1}=\varepsilon_{0}\varepsilon_{r1}\frac{A}{d_{1}}\:;\:C_{2}=\varepsilon_{0}\varepsilon_{r2}\frac{A}{d_{2}}\:and\:C_{3}=\varepsilon_{0}\varepsilon_{r3}\frac{A}{d_{3}}$$

从图中可以看出，这三个电容看起来像是串联连接的，所以

$$\frac{1}{C}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}=\frac{1}{(\varepsilon_{0}\varepsilon_{r1}\frac{A}{d_{1}})}+\frac{1}{(\varepsilon_{0}\varepsilon_{r2}\frac{A}{d_{2}})}+\frac{1}{(\varepsilon_{0}\varepsilon_{r3}\frac{A}{d_{3}})}$$

$$\Rightarrow\frac{1}{C}=\frac{d_{1}}{\varepsilon_{0}\varepsilon_{r1}A}+\frac{d_{2}}{\varepsilon_{0}\varepsilon_{r2}A}+\frac{d_{3}}{\varepsilon_{0}\varepsilon_{r3}A}=\frac{1}{\varepsilon_{0}A}(\frac{d_{1}}{\varepsilon_{r1}}+\frac{d_{2}}{\varepsilon_{r2}}+\frac{d_{3}}{\varepsilon_{r3}})$$

$$C=\frac{\varepsilon_{0}A}{(\frac{d_{1}}{\varepsilon_{r1}}+\frac{d_{2}}{\varepsilon_{r2}}+\frac{d_{3}}{\varepsilon_{r3}})}$$

$$一般情况下，C=\frac{\varepsilon_{0}A}{\sum(\frac{d}{\varepsilon_{r}})}$$

多层电容器的电容

为了获得更大的电容值，采用了多层结构。在这种结构中，电容器由交替的金属板和薄介质片构成。奇数号极板连接在一起形成一个端子A，偶数号极板连接在一起形成第二个端子B。

参考多层（在本例中为7层）电容器的示意图，它相当于6个并联的电容器。因此，总电容将是单个电容器电容的6倍。如果有n个极板，那么(n – 1)个电容器将并联连接。因此，

$$n-层电容器的电容=(n-1)\frac{\varepsilon_{0}\varepsilon_{r}A}{d}$$

其中，

• A为每个极板的面积，

• d为任意两个相邻极板之间的距离。

圆柱形电容器的电容

圆柱形电容器（例如电缆）由两个同轴圆柱体组成，由介质隔开。

参考示意图，圆柱形电容器的单位长度电容由下式给出：

$$C=\frac{2\pi\:\varepsilon_{0}\varepsilon_{r}}{log_{e}(\frac{D}{d})}\:F/m$$

如果电缆（圆柱形电容器）的长度为l米，则电缆的电容为

$$C=\frac{2\pi\:\varepsilon_{0}\varepsilon_{r}l}{log_{e}(\frac{D}{d})}\:法拉$$