电容单位

---

简介

在电路中，主要组成部分是电流、电压和电阻。电流是电荷的流动。电压电源作为这些电荷运动的能量来源。我们可以通过水流的例子来理解电势的概念。水总是从高处流向低处。势能在电场中是位置的函数，因此在不同的点具有不同的值。

对于单位电荷，势能称为电势。如果我们放置一个单位的电荷，它将从高电势移动到低电势。因此，电流总是从高电势流向低电势。我们也可以通过电路中的一些装置来储存这种静电能量。这种储存静电能量的新元件称为电容器。该元件储存能量的能力称为电容。

什么是电容器？

电容器由两个带相反电荷的导体组成，它们彼此非常靠近。这种导体排列被称为电容器。它可以在其极板之间产生静电能量。我们可以通过改变电容器的形状或在其间添加介电材料来增加其电容。

电容器可以有多种类型。下面列出了一些：

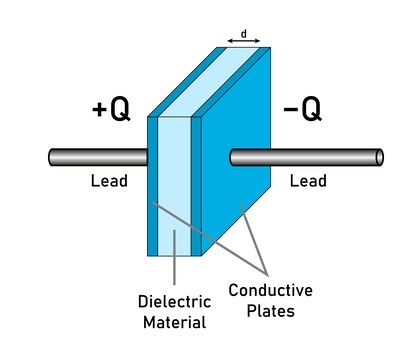
平行板电容器

平行板电容器有两个矩形导电板，它们之间保持一定的距离。

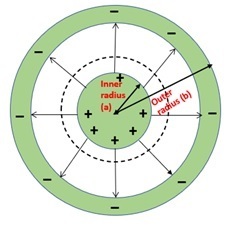
球形电容器

在球形电容器中，两个同心球形导电球体之间保持一定的距离。

圆柱形电容器

在圆柱形电容器中，两个同轴导电圆柱壳体之间保持一定的距离。

电容

储存电荷的能力称为电容。换句话说，对于电容器两端给定的电压，储存电荷的能力就是电容。

如果极板之间的电位差为 V，并且每个极板上的电荷分别为 +Q 和 -Q，那么我们发现极板上的电荷与电容器两端的电压成正比。

$$\mathrm{Q\:\propto\:V}$$

$$\mathrm{Q\:=\:C\:V}$$

这里 C = 电容

电容的单位和量纲公式

从上面的表达式，我们可以看到电容的单位。

$$\mathrm{C=\frac{Q}{V}}$$

$$\mathrm{C=1\:库仑/ 1伏特}$$

它将是库仑每伏特。

为了纪念迈克尔·法拉第，电容的 SI 单位称为法拉。法拉是一个非常大的电容单位，我们通常使用较小的电容单位。

$$\mathrm{1nF = 10^{−9} F}$$

$$\mathrm{1pF =10^{−12} F}$$

其量纲公式如下：

$$\mathrm{[C]=\frac{[Q]}{[V]}=\frac{[AT]}{[ML^{2} T^{−3} A^{−1}]}}$$

$$\mathrm{[C]=[M^{−1}L^{−2} T^{4} A^{2}]}$$

电容器的工作原理

当我们将电容器连接到电压源时，在电容器的极板之间会产生电场。电容器的一个极板连接到直流电源的正极，另一个极板连接到负极。因此，一个极板从电源收集正电荷，另一个极板收集负电荷。经过一段时间后，电容器的极板会充满电。电容器充满电所需的时间称为电容器的充电时间。

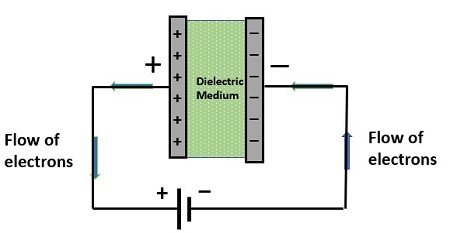
现在，如果我们断开电池，电容器的极板仍然会保持电荷。并且它们可以将电荷释放到连接到电路的一些负载上。电容器放电所需的时间称为放电时间。因此，电容器可以作为电能的临时来源。

计算电容器的电容

我们可以使用电容的定义来计算电容器的电容。

即

$$\mathrm{Q = CV}$$

这里我们以平行板电容器为例计算其电容。

假设极板之间的距离为 'd'，极板的电荷为 Q。极板的面积为 A。我们知道两个带电极板之间的电场为

$$\mathrm{\overrightarrow{E}=\frac{Q}{\epsilon_0A}}$$

电位差为 $\mathrm{V=Ed}$

我们可以用电荷表示电位 $\mathrm{V=d\frac{Q}{\epsilon_0 A}}$

因此，平行板电容器的电容为

$$\mathrm{C=\frac{\epsilon_0d}{A}}$$

应用

电容器可以以下列方式使用

• 在电路中，它可以用作临时电池。

• 滤波器可用于通过一定范围的频率。电容器用于滤波器电路。

• 用于传感器和信号处理。

• 它也用于整流器。

• 它用于平滑来自变压器或整流器的信号。

结论

电容是电容器储存电能的能力。它定义为总电荷量除以其两端的电位差。以法拉为单位进行测量。电容器由两个带相反电荷的导体组成，它们彼此非常靠近。这种导体排列被称为电容器。电容器用于许多电路中，例如整流器、变压器、滤波器等。主要有三种类型的电容器：平行板电容器、圆柱形电容器和球形电容器。

常见问题

Q1. 地球的电容是多少？

答：如果我们将地球视为一个球形电容器，则其电容将为

$$\mathrm{C=4\pi\epsilon_0 R}$$

其中 R = 6400 公里

$$\mathrm{C=4\pi\epsilon_0 R=4\times 3.14\times 8.854\times 10^{−12}\times 6400\times 10^3}$$

$$\mathrm{C=711\:\mu F}$$

Q2. 在介电材料存在的情况下，平行板电容器的电容是多少？

答：介电材料存在下的电容由下式给出

$$\mathrm{C=\frac{k\epsilon_0A}{d}}$$

其中 k= 介电常数。

Q3. 球形和圆柱形电容器的电容是多少？

答：

对于球形电容器

如果内球的半径为 $\mathrm{r_1}$，外球的半径为 $\mathrm{r_2}$，每个球上的电荷为 Q。

则球形电容器的电容可以写成

$$\mathrm{C = 4\pi\epsilon_0\frac{r_1r_2}{r_2-r_1}}$$

对于圆柱形电容器

如果圆柱体的长度为 l，内圆柱的半径为 $\mathrm{r_1}$，外圆柱的半径为 $\mathrm{r_2}$。每个壳上的电荷为 Q。则它们的电容将为

$$\mathrm{C=2\pi\epsilon_0\frac{1}{ln(\frac{r_2}{r_1})}}$$

Q4. 写出电容器静电能的表达式。

答：电容器的静电能取决于其两端的电压和电容。由下式给出

$$\mathrm{U=\frac{1}{2}CV^2}$$

其中 V = 电容器两端的电压

C = 电容器的电容

Q5. 在一个平行板电容器中，极板之间的距离为 6cm，每个极板的面积为 $\mathrm{30\:cm^{2}}$。如果我们在其两端施加 5V 的电压，则其电容是多少？

答：我们知道平行板电容器的电容为

$$\mathrm{C=\frac{\epsilon_0A}{d}}$$

$$\mathrm{C=\frac{8.85\times 10^{−12}\times 30\times 10^{−4}}{6\times 10^{−2}}}$$

$$\mathrm{C=8.85\times 10^{−12}\times 5\times 10^{−2}=4.43\times 10^{−14} F}$$

$$\mathrm{C=4.43\times 10^{−14} F}$$