数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究使用 Python 进行集总电容分析
当一个温度非常高的物体突然放入较冷的液体中，并且假设固体的导热阻力与周围的对流阻力相比非常小，那么传热分析被称为集总电容分析（如下面的图所示）。在这里，我们将系统视为一个整体。在这种情况下，我们可以假设集总内部能量的变化率将等于与周围流体的热相互作用。
数学上，这可以写成：
$$\mathrm{pcV\frac{\partial T}{\partial t} \: = \: − hA(T \: − \: T_{\infty}) \: \dotso\dotso \: (1)}$$
$$\mathrm{\frac{\partial T}{\partial t} \: = \: − \frac{hA}{pcV}(T \: − \: T_{\infty}) \: \dotso\dotso \: (2)}$$
现在需要求解方程 2 以获得温度随时间的变化。
如果我们将方程 2 从物体的初始温度 $\mathrm{T_{0}}$ 到某个任意温度 T 在时间 0 到 t 内进行积分，那么最终答案将是：
$$\mathrm{\frac{T \: − \: T_{\infty}}{T_{0} \: − \: T_{\infty}} \: = \: exp(− \frac{hA}{pcV}t) \: \dotso\dotso \: (3)}$$
现在可以以下列方式使用此方程：
如果需要达到某个温度 $\mathrm{T_{f}}$ 所需的时间：
$$\mathrm{t \: = \: − \frac{pcV}{hA}In(\frac{T_{f} \: − \: T_{\infty}}{T_{0} \: − \: T_{\infty}}) \: \dotso\dotso \: (4)}$$
如果需要在某个时间 $\mathrm{t_{f}}$ 时的温度：
$$\mathrm{T \: = \: T_{\infty} \: + \: (T_{0} \: − \: T_{\infty}) \: \times \: exp (−\frac{hA}{pcV}t_{f}) \: \dotso\dotso \: (5)}$$
让我们通过以下示例来演示这一点：
示例 1
一个半径为 1 毫米的钢球，温度为 $\mathrm{1200^{\circ}C}$，放置在温度为 $\mathrm{25^{\circ}C}$ 的露天环境中。计算将钢球冷却到 $\mathrm{100^{\circ}C}$ 所需的时间。$\mathrm{(k_{b} \: = \: 50 \: W/mK, \: c_{b} \: = \: 500kJ/kgK, \: p_{b} \: = \: 8000kg/m^{3}, \: and \: h_{air} \: = \: 10000W/m^{2}K)}$.
解答
由于需要计算时间，因此我们将使用方程 4。
# lumped capacitance analysis
from pylab import *
#Input Data
T_inf=25
r=1.E-3
T0=1200
Tf=100
k=50
c=500
ρ=8000
h=10000
#Evaluating Volume and Area
A=(4*pi*r**2)
V=(4/3)*pi*r**3
τ0=ρ*c*V/(h*A)
t=-τ0*log((Tf-T_inf)/(T0-T_inf))
print(f't = {round(t,3)} s')
输出
程序输出将是：
t = 0.367 s
示例 2
在示例 1 中，0.1 秒后钢球的温度是多少？
解答
在这种情况下，需要求解方程 5。除了公式外，其他一切都是相同的。
# lumped capacitance analysis
from pylab import *
# Input Data
T_inf=25
r=1.E-3
T0=1200
Tf=100
t=0.1
k=50
c=500
ρ=8000
h=10000
# Evaluating Volume and Area
A=(4*pi*r**2)
V=(4/3)*pi*r**3
τ0=ρ*c*V/(h*A)
T=T_inf+(T0-T_inf)*exp(-t/τ0)
print(f'T = {round(T,3)} deg. C')
输出
输出将是：
T = 580.031 deg. C
要理解图像，应该绘制温度的变化曲线。在这种情况下，将使用方程 3，如下所示：
示例 3
from pylab import *
# Input Data
T_inf=25
r=1.E-3
T0=1200
k=50
c=500
ρ=8000
h=10000
# Evaluating Volume and Area
A=(4*pi*r**2)
V=(4/3)*pi*r**3
# Evaluating time constant
τ0=ρ*c*V/(h*A)
t= linspace(0,1.0,50)
T=T_inf+(T0-T_inf)*exp(-t/τ0)
figure(1,dpi=300)
plot(t,T,'r-o')
xlabel('t (s)')
ylabel('T ($^\circ$C)')
savefig('plot1.jpg')
show()
输出
这是一个显示温度变化的曲线图：
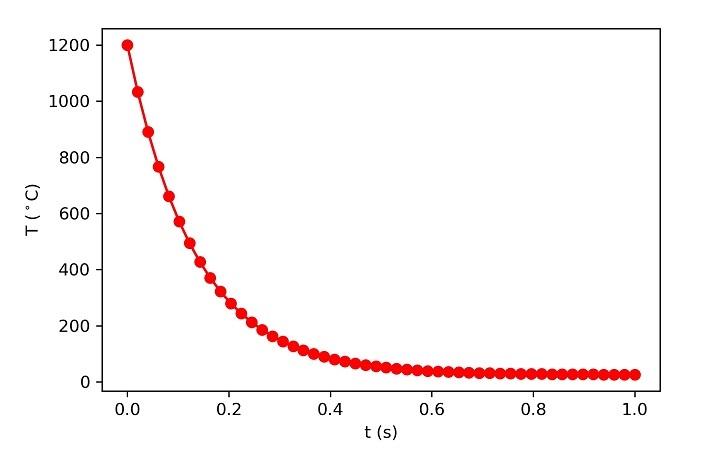
数值方法
如果要遵循数值方法，也可以这样做。让我们使用显式方法来求解方程 2。
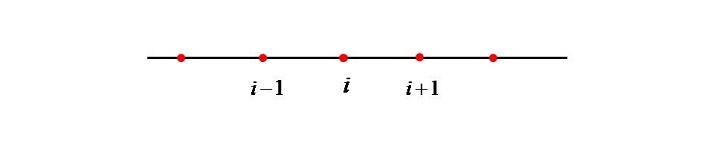
对于上面所示的网格，方程 2 可以离散化（使用前向差分）为：
$$\mathrm{\frac{T_{i} \: − \: T_{i − 1}}{\Delta t} \: = \: −\tau_{0}(T_{i} \: − \: T_{\infty})}$$
$$\mathrm{T_{i} \: = \: T_{i − 1} \: − \: \Delta t \: \times \: (T_{i} \: − \: T_{\infty})/\tau_{0} \: \dotso\dotso \: (6)}$$
下标表示时间步长。
我们将按时间推进，但在每个时间步长中，我们将迭代直到解决方案收敛。
由于在初始时间已知温度，即 1200，因此我们将从第二个时间步长开始。首先，我们将猜测此时间步长的温度值（例如 0），然后我们将求解方程 6，然后比较猜测值和获得的值。如果绝对差值小于收敛标准 $\mathrm{10^{− 5}}$，那么我们将移动到下一个时间步长。否则，我们将设置获得的温度值作为猜测值，并再次求解方程 6。重复此过程直到最后一个时间步长。下面的程序显示了此过程。我们还在其中将结果与精确的解析值（方程 3）进行了比较。
示例
from pylab import *
# Input Data
T_inf=25
r=1.E-3
T0=1200
k=50
c=500
ρ=8000
h=10000
# Evaluating Volume and Area
A=(4*pi*r**2)
V=(4/3)*pi*r**3
τ0=ρ*c*V/(h*A)
n=35 # Number of time steps
t = linspace(0,1.0,n)
Δt=1/(n-1)
# initial guess for all time steps
T=zeros(n)
# initial condition
T[0]=T0
# Array of guess
Tg=T.copy()
# Time marching
for i in range(1,n):
# Iteration loop
error=1
while error>1.E-5:
T[i]=T[i-1]-Δt*(T[i]-T_inf)/τ0
error=abs(T[i]-Tg[i])
Tg=T.copy()
# Exact solution
T_exact=T_inf+(T0-T_inf)*exp(-t/τ0)
# Data Plotting
figure(2,dpi=300)
plot(t,T,'r-o',label='Numerical')
plot(t,T_exact,'b-o',label='Analytical')
xlabel('t (s)')
ylabel('T ($^\circ$C)')
legend()
savefig('plot2.jpg')
show()
输出
程序输出如下：
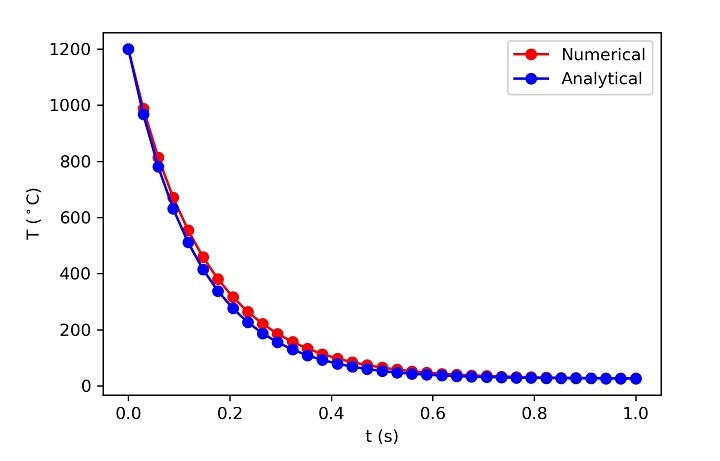
以下是生成上述图形的数据：
time T(analytical) T(numerical) 0.0 1200.0 1200.0 0.0294 987.6506 967.4051 0.0588 813.6776 780.853 0.0882 671.1455 631.2296 0.1176 554.3722 511.2245 0.1471 458.7025 414.9749 0.1765 380.3226 337.7781 0.2059 316.1076 275.8627 0.2353 263.4978 226.2036 0.2647 220.3958 186.3748 0.2941 185.0833 154.4301 0.3235 156.1526 128.809 0.3529 132.4503 108.2597 0.3824 113.0316 91.7782 0.4118 97.1223 78.5592 0.4412 84.0881 67.957 0.4706 73.4095 59.4535 0.5 64.6608 52.6334 0.5294 57.4932 47.1632 0.5588 51.6209 42.776 0.5882 46.8099 39.2572 0.6176 42.8684 36.4349 0.6471 39.6391 34.1713 0.6765 36.9935 32.3558 0.7059 34.826 30.8997 0.7353 33.0502 29.7319 0.7647 31.5954 28.7952 0.7941 30.4034 28.0439 0.8235 29.4269 27.4414 0.8529 28.6269 26.9581 0.8824 27.9714 26.5705 0.9118 27.4344 26.2596 0.9412 26.9945 26.0103 0.9706 26.634 25.8103 1.0 26.3387 25.6499
结论
在本教程中，已经使用 Python 解释并建模了集总电容分析。讨论了分析和数值方法。
199 次查看
