电场单位
引言
几乎所有物理学中的力都具有相关的“场”。简单来说,这个概念是为了提出一个量来衡量力的来源强度。
在物理学中,“场”指的是一种物理量,其特征是在空间和/或时间的不同点具有特定的值。它可以用标量或向量表示。在本教程中,我们将讨论一种称为电场的场类型及其测量单位。
什么是电场?
电场是一种存在于带电粒子周围的物理场,它对周围的其他带电物体施加力。这种力的性质取决于两个电荷的相似性,规则是同性电荷相互排斥,如同两块磁铁的同极。
电场可以由单个带电粒子、许多带电粒子的系统,甚至是由随时间变化的磁场产生。后一种情况是法拉第定律的结果。
可以通过将带电粒子所受的力除以其电荷来找到某一点的电场值。也就是说:
$$\mathrm{\overrightarrow{E}=\frac{\overrightarrow{F}}{q}}$$
虽然上述表示在大多数情况下足够,但在静电和电动力学中,通常更容易直接用电场来表示问题。电场的更好表示是根据电势,我们用电势表示电场为:
$$\mathrm{\overrightarrow{E}(\overrightarrow{r})=-\frac{dV}{dr}}$$
因此,电场的另一个定义是:“电势的负梯度给出电场”。
电场的SI单位
为了推导出电场的SI单位,我们可以使用它的定义。由于它是电势的梯度(负),因此它的SI单位只是伏特每米(V/m)。
就基本单位而言,分子中的伏特可以展开,从而给出电场的基表示为$\mathrm{m\cdot kg \cdot s^{−3}\cdot A^{−1}}$
电场的导出单位
可以从电场的其他定义推导出电场的其他单位。因此,V/m单位相当于N/C。
最常用的是我们使用V/m的SI单位来讨论电场。就数值而言,N/C和V/m是相等且可以互换的。
电场的重要性
表征电荷系统
当我们讨论系统本身时,可以单独处理电荷系统中的每个电荷。但是,要了解该系统作为一个整体对其他电荷的影响,单独处理每个电荷是没有意义的。
电场是一个矢量量,遵循叠加原理。因此,使用矢量加法,我们可以将系统中每个电荷的电场值相加,并找到净电场。然后,可以使用此净电场来描述系统对周围电荷的影响。
静电和电动力学问题
麦克斯韦方程组构成了电动力学的基石,它们使用电场和磁场处理所有问题。因此,用类似的术语陈述我们的问题陈述更有意义。这使得进一步的处理和计算更容易。因此,电场广泛出现在静电和电动力学问题中。
我们周围存在的电场
在无数情况下都会遇到电场。但最有趣的一点是,如果没有电场,这个世界将不复存在!原因如下:我们知道原子是由原子核和周围的电子组成的。这些电子由原子核中质子的场保持在适当位置。如果这个电场消失,电子就会从原子中飞出,整个宇宙就会陷入混乱。
电场线
如果您曾经看过天气地图,您会记得风的流动是用箭头和线表示的。这不是必要的,但这使得更容易理解风流模式。类似地,电场可以用在空间中绘制带箭头的线来表示。
这些线完全是想象出来的,仅作为理解电场如何在空间区域内分散的视觉辅助工具。电场的方向由箭头的方向给出,而线的长度表示大小。由于电场不能有多个方向,因此我们永远不会有两条电场线相互交叉。
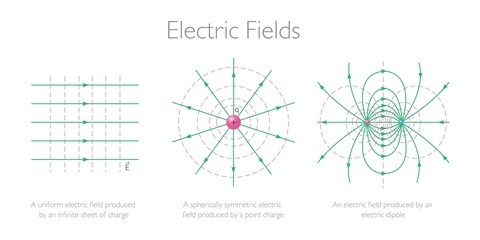
电场线的起点总是在正电荷处。但是,线可能以负电荷甚至无穷远结束。也就是说,电场线(以及因此电场本身)的方向是从正电荷径向向外,从负电荷径向向内。
结论
在数学上,电场只是每单位电荷所经历的力的大小。另一个根据电势的定义如下:电场是电势的负梯度。
根据上述定义,可以找出电场的SI单位,即伏特每米(V/m)。这个单位相当于库仑每牛顿,可以使用这两个单位中的任何一个。电场线的起点总是在正电荷处。但是,线可能以负电荷甚至无穷远结束。也就是说,电场线的方向是从正电荷径向向外,从负电荷径向向内。
常见问题
Q1. 电场的正式定义是什么?
A1. 在某一点上,一个极小、正的、静止的单位电荷(且不影响源电荷)所受到的力被称为该点的电场。
Q2. 自然界中还存在哪些类型的场?
A2. 几乎所有力都可以用场来表征。引力场、磁场、核场等是常见的例子。
Q3. 电场线和力线之间有区别吗?
A3. 没有。术语“力线”最初是由法拉第提出的,他首先提出了场线的概念。
Q4. 有没有一种简单的方法来计算某一点的电场?
A4. 高斯定律是一种非常容易计算电场的方法。它描述了从任何任意表面流出的电通量与封闭在其中的总电荷之间的关系。数学上,
$$\mathrm{\int\:\overrightarrow{E}\cdot\:d\overrightarrow{a}=\frac{q}{\epsilon_0}}$$
这里,q是选定表面内封闭的总电荷。
Q5. 电场遵循哪个数学定律?
A5. 电场遵循平方反比定律,就像电力一样。万有引力也遵循相同的定律,在一定限度内,核力也遵循相同的定律。


 数据结构
数据结构 网络
网络 关系型数据库管理系统(RDBMS)
关系型数据库管理系统(RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C语言编程
C语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP