电力及电气设备效率

功率或电功率

在电路中做功的速率称为电功率。换句话说，单位时间内所做的功称为电功率。用p或P表示。

功率的公式和单位

当电压加在电阻两端时，会引起电流通过它。因此，在单位时间内使电子穿过电阻所做的功称为电功率。

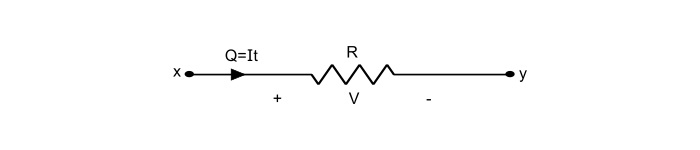
参考上图，

$$\mathrm{V=\frac{功}{Q}}$$

$$\mathrm{\Rightarrow 功(W)=VQ=VIt}$$

由于功率定义为单位时间内所做的功，即

$$\mathrm{功率(P)=\frac{电路中所做的功(W)}{时间(t)}=\frac{VIt}{t}}$$

$$\mathrm{(∵V=IR\:或\:I=\frac{V}{R})}$$

$$\mathrm{∴P=VI=I^2R=\frac{V^2}{R}}$$

以上三个公式都可用于计算功率。使用哪个公式取决于已知量。

由于功的单位是焦耳，时间的单位是秒。因此，功率的单位是焦耳/秒或瓦特，即

$$\mathrm{功率单位=\frac{焦耳}{秒}=瓦特}$$

因此，如果1 V的电压使1 A的电流流过电路，则该电路消耗的功率为1瓦。

功率的较大单位有千瓦(kW)、兆瓦(MW)和吉瓦(GW)。

$$\mathrm{1\:kW=1000\:W;1MW=10^6\:W=10^3\:kW;1\:GW=10^9W}$$

有时，功率也用马力(h.p.)来衡量，

             1 马力 (h.p.) = 746 瓦特

功率的表达式

• 功率在平动系统中的表达式，

$$\mathrm{功率=\frac{所做的功}{时间}=\frac{力×距离}{时间}=力×速度}$$

• 功率在转动系统中的表达式，如果一个物体以N转/分的速度旋转，作用在其上的扭矩为τ牛顿·米，则，

$$\mathrm{每分钟所做的功 = 2\pi Nτ\:焦耳}$$

$$\mathrm{每秒所做的功 =\frac{2\pi Nτ}{60}焦耳/秒}$$

因此，

$$\mathrm{功率(P)=\frac{2\pi Nτ}{60}焦耳/秒\:或\:瓦特}$$

$$\mathrm{(∵\:746\:瓦特 = 1 马力 )}$$

$$\mathrm{∴\:功率\:(P)=\frac{2\pi Nτ}{60×746}马力}$$

电气设备的效率

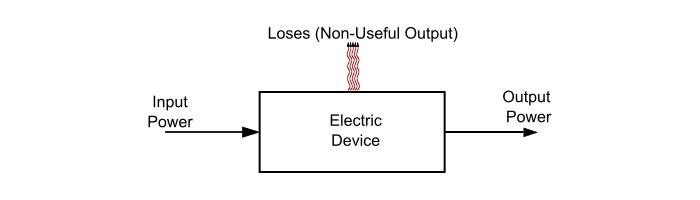
电气设备的效率定义为有用输出功率与输入功率之比，即

$$\mathrm{效率(\eta)=\frac{有用输出功率(P_{o})}{输入功率(P_{i})}}$$

由于效率是输出功率和输入功率之比，因此它是一个无量纲量。通常，设备的效率以百分比（%）表示，如

$$\mathrm{\%\:效率(\eta)=\frac{有用输出功率(P_{o})}{输入功率(P_{i})} × 100 \%}$$

一些电气设备的效率接近100%。例如电加热器，其中所有输入电能都转换为热能。

低效率的有害影响

低效率的有害影响如下：

• 设备效率低意味着损失越大，因此大量能量浪费在无用输出上。

• 无用输出以热量的形式出现，从而提高设备的温度。因此，效率低意味着温度升高显著。运行温度过高的设备更容易出现故障。

• 由于效率低而产生的热量必须散发掉。因此，散热系统增加了设备的成本和尺寸。

数值示例 - 1

一台电动机在1500转/分的速度下产生60牛米·米的扭矩。计算该电动机以瓦特和马力表示的输出功率。

解答

$$\mathrm{电动机输出功率,P=\frac{2\pi Nτ}{60}=\frac{2\pi×1500×60}{60}=9420 W}$$

$$\mathrm{(∵\:746\:瓦特 = 1 马力 )}$$

$$\mathrm{∴p=\frac{功率（瓦特）}{746}=\frac{9420}{746}=12.63 马力}$$

数值示例 - 2

一台质量为200千克的升降机以10米/秒的速度上升。如果驱动电机的输入功率为21.42千瓦。计算电机的百分比效率。

解答

             升降机的重量，F = mg = 200 × 9.81 = 1962 牛顿

   电动机的输出功率 = 力 × 速度 = 1962 × 10 = 19620 瓦 = 19.62 千瓦

$$\mathrm{\%\:效率=\frac{电动机输出功率}{电动机输入功率}× 100\:\%\:=\frac{19.62}{21.42}× 100 = 91.59\%}$$

数值示例 -3

一个100欧姆的电阻器两端电压为120伏。计算电阻器吸收的功率。

解答

电阻器吸收的功率，

$$\mathrm{p=\frac{V^2}{R}=\frac{(120)^2}{100}=144 W}$$

Manish Kumar Saini

更新于: 2021年8月30日

1K+ 浏览量

启动你的 职业生涯

通过完成课程获得认证

开始学习