频率单位

---

介绍

波是在介质中传播能量而不传播质量的扰动。波通常以周期性运动的形式存在，例如简谐振荡器。它们有波峰和波谷。

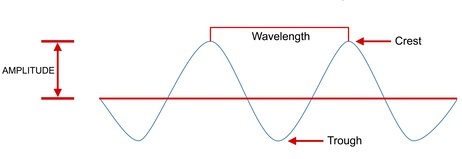
波的振幅是波的高度。两个连续波峰之间所覆盖的距离称为波长。每秒通过的波数称为波的频率。相位不是波的属性。但它给出了两个具有相同频率的信号之间的关系。

现在，我们将讨论波、低频波和高频波及其单位。

什么是频率？

在特定时间内通过某一点的波数称为频率。它也表示为每单位时间的振动次数或循环次数。如果一个物体处于周期性运动中，它会完成一个完整的事件并返回到其原始位置。波的频率是完成一个循环所需时间间隔的倒数。

音叉的叉臂以特定的频率来回振动。频率通常与振动、振荡和旋转等过程相关。频率用 f 表示。频率是音频信号、机械振动、光和无线电波中的一个重要因素。

频率单位

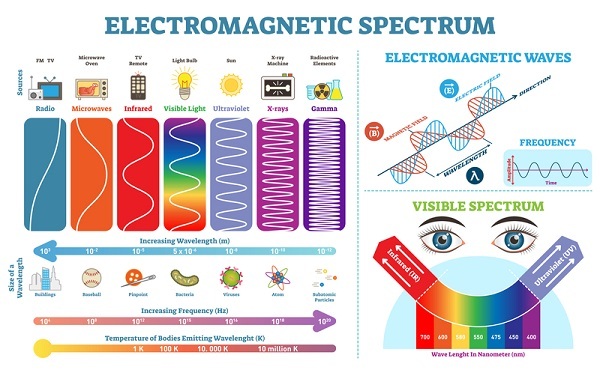
频率的单位是赫兹。每秒一次振动或振荡表示为一赫兹。通过空气传播的声波会使气压发生变化。这种气压会被人类和生物的耳朵检测到，从而捕捉到声音。通常，人类可听到的声波频率范围在 20Hz 到 20000 Hz 之间。

次声波的频率低于人类可听范围的频率。即小于 20 Hz。超声波的频率高于人类可听范围的频率。即大于 20000 Hz。由频率引起的感知称为音调。如果声波的频率高，则音调也高，反之亦然。

$$\mathrm{1\:赫兹=1\:振动\:秒^{−1}}$$

一千赫兹等于 1000 赫兹，1 兆赫兹等于 106 赫兹，1 吉赫兹等于 10⁹ 赫兹。在光谱学中，频率以波数来测量。每单位距离的波数称为波数。在机械装置中，它计算为每分钟转数 (rpm)。

$$\mathrm{1\:赫兹 = 60\:rpm}$$

根据粒子的周期性运动，频率分为两种。它们是空间频率和角频率。

空间频率

粒子的空间频率受空间坐标控制。空间频率是任何周期性结构的特征。粒子的空间频率与振动粒子的波长成反比。空间辐射的测量以米/弧度为单位。

角频率

进行旋转运动的粒子与角频率相关。它由粒子在特定时间内完成的旋转次数定义。角频率的单位也是赫兹。角频率用 $\mathrm{\omega}$ 表示。频率和角频率表示为：

$$\mathrm{f=\frac{\omega}{2\pi}}$$

$\mathrm{\omega}$ 表示粒子的角频率。

因此，角频率由下式给出：

$$\mathrm{\omega=2\pi f}$$

频率公式

根据已知量，计算频率的公式分为三种。

公式-1

粒子的频率是粒子振荡周期的倒数，表示为

$$\mathrm{f=\frac{1}{T}}$$

这里 f 表示粒子的频率。

这里 T 表示粒子完成一个循环所需的时间。

公式-2

频率也指波的速度与波长的比率，表示为：

$$\mathrm{f=\frac{速度}{波长}}$$

$$\mathrm{f=\frac{
u}{\lambda}}$$

这里 v 表示波的速度

这里 $\mathrm{\lambda}$ 表示波长。

公式-3

频率也可以通过进行旋转运动的粒子的角速度来计算，表示为：

$$\mathrm{f=\frac{\omega}{2\pi}}$$

例题

1. 波长为 400 nm 的光波的频率是多少？

已知

$$\mathrm{波长= \lambda=400 \times 10^{−9}m}$$

$$\mathrm{光速\:c=3 \times 10^{8}\: m/s}$$

光波的频率 $\mathrm{= f=\frac{c}{\lambda}}$

$$\mathrm{f=\frac{3 \times 10^{8}}{400 \times 10^{−9}}}$$

$$\mathrm{f=\frac{3}{400}\times 10^{8}\times 10^{9}}$$

$$\mathrm{f=0.75\times 10^{−2}\times 10^{8}\times 10^{9}}$$

$$\mathrm{f=0.75 \times 10^{15}}$$

$$\mathrm{f=7.5 \times 10^{14}\:Hz}$$

因此，光波的频率为 $\mathrm{f=7.5\times\:10^{14}\:Hz}$

2. 计算一个摆完成一个循环需要 5 秒的频率。

已知：所需时间 = T =5 秒

摆的频率为 $\mathrm{f=\frac{1}{T}}$

$$\mathrm{f=\frac{1}{5}}$$

$$\mathrm{f=0.2\:Hz}$$

摆的频率为 0.2 Hz。

结论

在本教程中，讨论了关于频率、频率单位和角频率的事实。还讨论了频率公式和一些例题。

常见问题

Q1. 什么是频率调制？

答：如果瞬时信号电压发生变化，则载波频率会发生变化。这称为频率调制。因此，载波的幅度和相位不会发生变化。

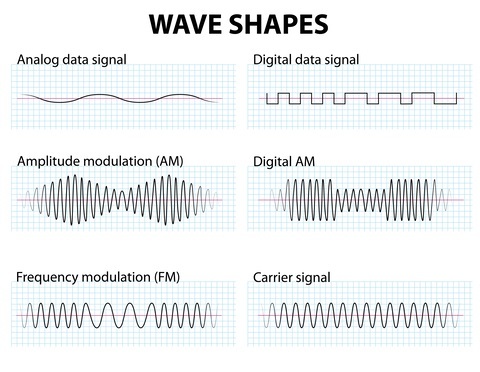
Q2. 给出 FM 调制的应用

答：频率调制应用于雷达和脑电图监测电路。它主要用于 FM 广播。它也应用于磁带录音系统。它在卫星和微波通信、蜂窝无线通信和电视声音传输中具有广泛的应用。

Q3. 频率调制的应用有哪些？

答：频率调制用于研究振荡现象、音频波、无线电波和光波的振动现象。频率公式用于测量波长、频率、波速、周期和一些其他相关公式。

Q4. 幅度调制和频率调制有什么区别？

答：

幅度调制	频率调制
根据载波信号变化幅度	根据载波信号变化频率
频率和相位保持恒定	幅度和相位保持恒定
音质差	音质好
与 FM 相比，它不太复杂	它更复杂。
带宽较小	带宽较大
传输过程中浪费功率	它效率很高，因为所有功率都得到了利用。

Q5. 如何测量频率？

答：有两种类型的仪器用于测量频率，例如转速表和振荡器。Fullarton 转速表和 Frahm 转速表是用于测量频率的转速表类型。石英振荡器、铷振荡器和铯振荡器是振荡器类型。在普通的电路中，频率由数字万用表、功率分析仪和示波器测量。