数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学晶胞密度
引言
晶胞的质量与晶胞体积之比称为晶胞密度。晶胞的质量等于晶胞中原子个数乘以每个原子的质量。
晶胞是固体中最紧凑且最基本的重复结构单元，用于表示固体的晶体结构。这种可视化也有助于计算晶胞密度。晶胞重复形成网络，称为晶格，晶格中的粒子在空间中表示为点。晶胞有多种形状，取决于边角之间的角度和边长。固体的整体对称性取决于晶胞的类型。通过了解晶胞的晶格结构，可以轻松计算晶胞密度。
什么是晶胞？
固体的结构是三维排列的，它们的排列具有重复单元。因此，每个固体结构单元中最小的重复单元称为晶胞。晶胞的重复形成晶体。根据排列类型，晶胞有多种类型。主要晶胞和非主要晶胞是两大类。
当构成粒子仅位于角顶时，称为简单晶胞（或称原始晶胞）。如果构成粒子既位于角顶又在其他位置，则为非主要晶胞。晶胞有六个参数：三个角之间的角度 (α、β 和 γ) 和三个边长 (a、b 和 c)。
可视化的益处
固体晶体结构的可视化非常重要。它可以用来解释：
固体的性质。
帮助识别堆垛方式。
帮助识别扩展结构。
了解固体的离子晶格。
给出固体的实验式。
从可视化中获得单个晶胞的知识。
什么是晶格？
固体中原子或离子的三维空间排列称为晶格。为了降低总的分子间能量，固体中的原子以某种几何形状排列，这就是固体的晶格结构。因此，它是一种示意图表示，包括原子、离子和分子。构成粒子用点表示，称为晶格点。通过直线连接这些点形成晶格的几何形状。
布拉维晶格
如果在晶格中，周围的晶格点都相同，或者所有粒子都相同，则称为布拉维晶格。在这样的晶体中，原子的排列方向也相同。1848年，布拉维指出，描述晶体只需要14种晶格，这就是布拉维晶格。根据布拉维晶格的晶胞参数，共有7种晶系，它们是：
三方晶系（或菱方晶系）
四方晶系
三斜晶系
单斜晶系
立方晶系
六方晶系
正交晶系
晶胞密度计算
晶胞密度是晶胞质量与晶胞体积之比。我们可以用以下公式简单地计算它。
$$\mathrm{密度,\rho\:=\:质量\: / \:体积}$$
晶胞质量可以用以下公式计算：
$\mathrm{晶胞质量\:=\:晶胞中原子个数\:\times\:每个原子的质量\:}$
$$\mathrm{m\:=\:M/N_{A},\:其中\:M\:=\:摩尔质量}$$
体积可以通过晶胞的边长计算得出。如果a是边长，则体积是：
$$\mathrm{V\:=\:a^{3}}$$
$\mathrm{所以,\:密度,\:\rho\:=\:z\:\times\:m/a^{3}\:=\:\frac{z\:\times\:M}{N_{A}a^{3}}}$
示例
一种具有体心立方晶体结构的化合物，原子质量为50 amu，边长为290 pm。计算晶胞的密度（单位为gcm⁻³）。
答案：计算密度的公式为$\mathrm{\rho\:=\:z\:\times\:m/a^{3}\:=\:\frac{z\:\times\:M}{N_{A}a^{3}}}$
体心立方的原子数为2(z)。
$$\mathrm{\rho\:=\:\frac{2\:\times\:50}{6.022\:\times\:10^{23}\:\times\:(290\:\times\:10^{-10})^{3}}\:=\:6.81\:gcm^{-3}}$$
因此，密度为$\mathrm{6.81\:gcm^{-3}}$
该技术的意义
晶胞密度计算公式具有一定的意义，例如：
当已知其他所有因素时，可用于计算边长。
如果已知密度，也可用于计算晶胞的体积。
也可用于计算晶胞的质量。
可用于计算多种晶体的密度。
各种情况下晶胞密度的一般表达式
计算晶胞密度的一般公式为：
$$\mathrm{\rho\:=\:z\:\times\:m/a^{3}}$$
面心立方（FCC）晶胞中(110)平面的平面密度是多少？
单位面积上原子的数量是平面密度。FCC 110的平面密度为：
$\mathrm{\:\:\:\:\:平面密度\:=\:\frac{原子数}{平面面积}}$
$\mathrm{\:\:\:\:\:\:\:\:=\:0.177/\:(构成粒子的半径)^{2}}$
已知构成原子的半径，就可以计算平面密度。
简单晶胞
当构成粒子仅存在于晶格点（即立方体的8个顶点）时，称为简单晶胞。因此，它只包含一个晶格点。它是所有其他晶体结构的基本晶胞，因为在这个晶胞上添加一些原子会导致其他晶胞的形成。
体心立方晶胞
这是非主要晶胞的一种分类。立方体的八个角上都有原子，中间还有一个原子，从而构成体心立方晶胞。体心立方晶胞的配位数为8。原子总数为2，中心一个，八个角各一个。
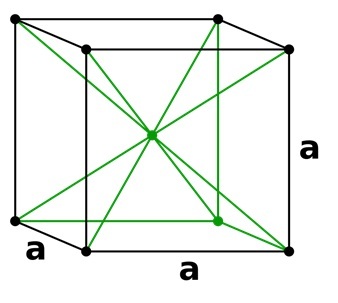
Mih.s29 , 体心立方晶格 , CC BY-SA 4.0
面心立方晶胞
这也是一种非主要晶胞。在这种晶胞中，立方结构的八个角上各有一个原子，每个面的中心也各有一个原子。这种晶胞的配位数为12。原子总数为4。
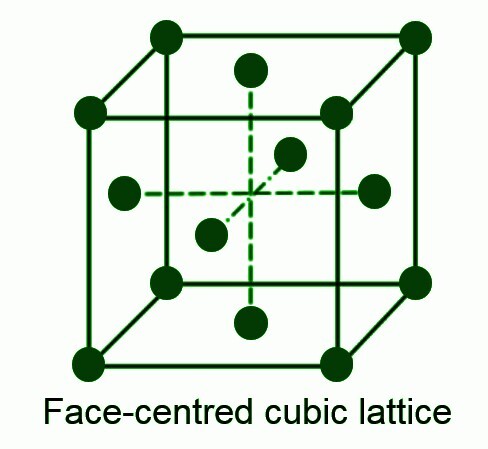
关于晶胞
就像生物体由细胞构成一样，我们周围的所有晶体都由称为晶胞的最小的重复单元构成。因此，它是每种晶体的基本组成部分。晶胞也代表结构的对称性。它们以适当的方式排列，以获得每种晶体的完美形状。
晶格常数和密度之间关系的解释
晶格常数是所有晶格的参数。边长a、b和c是参数。它与密度计算的关系如下式所示：
$$\mathrm{\rho\:=\:z\:\times\:m/(晶格常数)^{3}}$$
金刚石晶体结构
金刚石是一种具有面心立方布拉维晶格的立方结构，由碳元素构成。因此，立方结构的八个角上和所有面的中心各有一个原子。因此，原子总数为4。因此，金刚石包含面心立方晶格的重复单元。
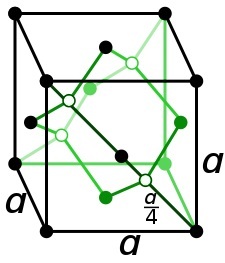
结论
晶胞是每种晶体中最小的重复单元。晶胞赋予晶体对称性和形状。原子的三维排列导致晶格的形成。晶胞有两种类型：主要晶胞和非主要晶胞。晶胞有六个参数：三个角度和三个边长。每种晶胞的密度都用公式ρ = z × m/a³计算。晶格常数a与密度计算有关。共有七种晶系，称为布拉维晶格。金刚石的立方结构是面心立方晶格。
常见问题
1. 什么是底心晶胞？
这是一种非主要晶胞，其中粒子存在于8个角上和两个相对面的中心。因此，原子总数为2。
2. NaCl是体心立方结构吗？
NaCl是面心立方结构，包含四个钠原子和四个氯原子。
3. hcp的例子是什么？
许多元素金属具有hcp（六方密堆积）结构。例如，钛、锌等。
4. 什么是简单立方晶格？
简单立方晶格是最简单的晶胞。它只包含立方体角上的原子。因此，它也称为简单立方。
5. 金金属是简单立方晶胞吗？
金金属是面心立方晶格。所有金原子都排列为面心立方（FCC）晶格的重复单元。
浏览量：229
