晶胞堆积效率

---

介绍

晶胞堆积效率指的是任何特定结构或晶胞中组成部分粒子的排列，以及原子之间存在空隙的情况。晶胞堆积是通过任何特定体积来获得的，该体积由构成晶胞的粒子占据，并与晶胞的总体积相关。晶胞堆积效率通常用百分比值来表示。

关于晶胞堆积效率的信息

晶胞被描述为具有三个维度的结构，并由一个或多个原子构成。此外，可以使用 3D 对象来可视化晶胞。当晶胞发生堆积时，会发现其中存在一定的空隙。

该空间被其他组分或粒子填充。用特定晶胞或结构填充的绝对空间的比例称为填充率。在化学中，百分比视图对于了解构成粒子的有效性至关重要。该结构的概念提供了关于化学中晶胞堆积的有效知识。

晶格指的是大量构建的晶胞，其中晶格点要么被填充，要么被构成粒子占据。晶胞的晶格点是一个概念，它寻求一个三维结构，也称为 3D 结构。

面心立方或密堆积 (ccp) 和六方密堆积 (hcp) 是两种在化学中考虑堆积时的有效晶格。这两种堆积都指的是 74% 的空间被填充。例如，立方晶格的堆积效率为 52.4%，体心立方晶格 (bcc) 的堆积效率为 68%。

体心立方 (BCC) 晶胞的堆积效率

BCC 是一种原子排列方式，指的是粒子位于盒状结构的八个边角上，以及一个粒子位于盒状结构的中心。以下公式考虑了计算效率的过程，该过程基于以下表达式：

$$\mathrm{半径或r =\sqrt{\frac{3}{4}}\:a}$$

此外，上述公式包含两个原子，一个原子占据的面积为 $\mathrm{\frac{4}{3}}$。BCC 堆积的效率被认为是 68.04%，其余 32% 的体积仍然是空隙。

简单立方晶胞的堆积效率

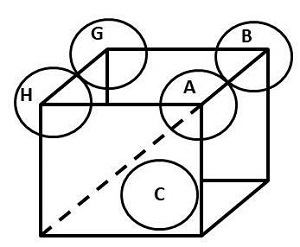
图 1：体心立方晶胞中的堆积效率

$$\mathrm{r=\frac{a}{2}}$$

$$\mathrm{a=2r}$$

因此，堆积效率 = 一个原子占据的体积 / 晶胞的总体积 × 100。

$$\mathrm{堆积效率 = \frac{4}{3}r^3 / (2r^3 \times\:100)}$$

因此，简单立方晶胞 (SCC) 的堆积效率为 52.4%。

六方密堆积 (HCP) 和面心立方密堆积 (CCP) 的堆积效率

HCP 和 CCP 都指的是具有相同堆积效率的结构，两者之间的关系表示为半径表示为 r。

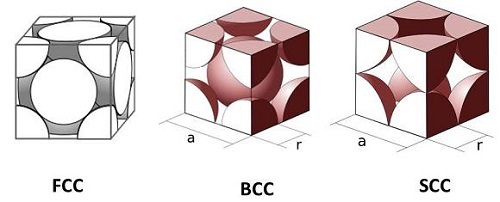
图 2：FCC、BCC 和原子简单堆积的效率

Cubique_centre_atomes_par_maille.svg: Cdang（原始构思和 SVG 执行），Samuel Dupré（使用 SolidWorks 进行 3D 建模）衍生作品：Daniele Pugliesi（讨论），CCC 晶胞（不透明），CC BY-SA 3.0

Cdang，Cubique a faces centrees atomes par maille，CC BY-SA 3.0

CCC_crystal_cell_(opaque).svg: *Cubique_centre_atomes_par_maille.svg: Cdang（原始构思和 SVG 执行），Samuel Dupré（使用 SolidWorks 进行 3D 建模）衍生作品：Daniele Pugliesi（讨论）衍生作品：Daniele Pugliesi（讨论），简单立方晶胞（不透明），CC BY-SA 3.0

以下等式指的是这两种堆积技术在溶液中的用例：

$$\mathrm{a = \sqrt{2r}}$$

这些块被称为立方体的面心晶格点，它包含一些额外的原子，这些原子位于立方体的八个角上以及每个壁的中心。体积用 r 表示，方程可以表述为以下内容：

$$\mathrm{(2\sqrt{2}r)^3 = 16\sqrt{3}{2r}^3}$$

HCP 和 CCP 的堆积效率指的是空隙空间占 26%。

结论

晶胞指的是构成晶体时分子或原子的最小集合，当它们在 3D 空间中以规则间隔排列时。晶胞中堆积效率指的是原子或离子占据位置的总体积与空隙区域的比例。六方密堆积指的是通过组织和聚焦于晶胞构建的立方结构。

常见问题

Q1. 什么是堆积效率？

A1. 在某种堆积中，粒子占据的总体积的百分比被称为堆积效率。构成晶体的原子、离子和其他粒子紧密地堆积在晶格中。它们可以在 ccp 或 hcp 内部进行，具体取决于现象。在这两种情况下，都指的是空隙的数量，即未被占据的总空间。

Q2. HCP 和 CCP 结构的堆积效率是多少？

A2. CCP 和 FCC 的堆积效率是面心立方结构。八面体空隙中的原子被称为立方密堆积 (ccp)，其效率为 74%。此外，还有两种不同的名称可以帮助理解堆积效率的知识。

Q3. CCP 和 FCC 是否相同？

A3. CCP 和 FCC 是立方应力，指的是关于晶胞中原子堆积的知识发展。堆积的空隙指的是 ABCABC 形式，被称为 CCP，晶胞是 FCC。

Q4. 晶胞中 BCC 堆积的过程是什么？

A4. 在化学中添加 BCC 堆积提供了关于每个角有八个原子和一个原子放置在中心的过程的知识。BCC 结构在晶胞堆积效率方面是开放的。该方程指的是 8 × 1/8 = 1 个原子。

Q5. SCC 的堆积效率是多少？

A5. SSC 的堆积效率在化学中的晶胞堆积中约为 52.4%。