直流电动机的效率 - 最大效率的条件

直流电动机的效率

直流电动机的效率定义为输出功率与输入功率之比。

数学上，

$$\mathrm{效率,\eta \:=\:\frac{输出功率}{输入功率}\times 100 \%\:=\:\frac{P_{out}}{P_{in}}\times100\%\:...(1)}$$

由于，

$$\mathrm{输入功率,\:P_{in} = 输出功率(P_{out}) + 损耗}$$

因此，

$$\mathrm{效率,\eta \:=\:\frac{P_{out}}{P_{out}\:+\:损耗}\times100\%\:....(2)}$$

直流电动机最大效率的条件

直流电动机的效率不是恒定的，而是随负载变化。考虑一个并励电动机（如图所示），其电枢电流为 I_a 安培，反电动势为 E_b。

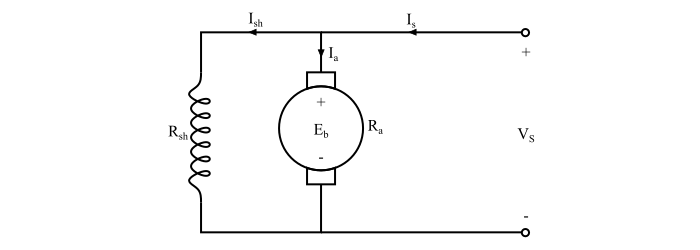
电动机产生的机械功率（忽略机械损耗）为：

$$\mathrm{P_{m}=P_{out}=E_{b}I_{a}}$$

电动机的输入功率为：

$$\mathrm{P_{in}=P_{out}\:+\:可变损耗\:+\:恒定损耗}$$

$$\mathrm{效率,\eta\:=\:\frac{P_{out}}{P_{in}}\:=\:\frac{E_{b}I_{a}}{P_{out}\: +\:可变损耗\:+\:恒定损耗}}$$

$$\mathrm{⇒\eta\:=\:\frac{E_{b}I_{a}}{E_{b}I_{a}\:+\:I_a^2R_{a}\:+\:W_{c}}}$$

$$\mathrm{⇒\eta\:=\:\frac{1}{1+(\frac{I_{a}R_{a}}{E_{b}})+\frac{W_{c}}{E_{b}I_{a}}}\:....(3)}$$

如果公式 (3) 的分母最小，则电动机的效率将最大。因此，为了确定最大效率的条件，需要对公式 (3) 的分母相对于电枢电流进行微分，并将其等于零，即

$$\mathrm{\frac{d}{dt}[1+(\frac{I_{a}R_{a}}{E_{b}})+(\frac{W_{c}}{cd})]\:=\:0}$$

$$\mathrm{⇒\:(\frac{R_{a}}{E_{b}})\:-\:(\frac{W_{c}}{E_{b}I_a^2})\:=\:0}$$

$$\mathrm{⇒\:\frac{R_{a}}{E_{b}}\:=\:\frac{W_{c}}{E_{b}I_a^2}}$$

$$\mathrm{⇒\:I_a^2R_{a}\:=\:W_{c}}$$

$$\mathrm{⇒\:可变损耗\:=\:恒定损耗 … (4)}$$

因此，当电动机的可变损耗等于恒定损耗时，直流电动机的效率最高。

对应于最大效率的电枢电流由下式给出：

$$\mathrm{I_{a}=\sqrt\frac{W_{c}}{R_{a}}\:\:......(5)}$$

数值示例

一台 10 kW 的直流并励电动机在满载时的损耗如下：

机械损耗 = 300 W

铁损 = 400 W

励磁绕组铜损 = 100 W

电枢铜损 = 500 W

如果电枢电阻为 0.25 Ω，计算电动机的满载效率和对应于最大效率的电枢电流。

解答

这里，

$$\mathrm{恒定损耗,\:W_{c}\:=\:300 + 400 + 100\:=\:800 W}$$

$$\mathrm{可变损耗\:=\:电枢铜损\:=\:500 W}$$

$$\mathrm{总损耗\:=\:800 + 500\:=\:1300 W}$$

因此，

$$\mathrm{输入功率,P_{in} = 10000 + 1300 = 11300 W}$$

$$\mathrm{\therefore \:效率,\eta \:=\:\frac{P_{out}}{P_{in}}\times100\:=\:\frac{10000}{11300}\times 100 \:}$$

$$\mathrm{⇒\:\eta\:=\:88.49\%}$$

对应于最大效率的电枢电流，

$$\mathrm{I_{a}\:=\:\sqrt\frac{W_{c}}{R_{a}}\:=\:\sqrt\frac{800}{0.25}\:=\:56.57A}$$

Manish Kumar Saini

更新于: 2021 年 8 月 16 日

10K+ 浏览量

开启你的 职业生涯

通过完成课程获得认证

开始学习