如何测试直流电机效率？（霍普金森试验）

霍普金森试验是一种测试直流电机效率的方法。霍普金森试验也称为再生试验、背靠背试验或热运行试验。

此测试需要两台相同的并励电机，它们机械连接并电气并联。一台电机作为电动机，另一台作为发电机。

电动机从电源获取输入，电动机的机械输出驱动发电机。发电机的电输出用于向电动机供电。因此，每台机器的输出都作为另一台机器的输入。

当两台机器都以额定负载运行时，来自电源的输入等于两台机器的总损耗。因此，来自电源的功率输入非常小。

连接图

霍普金森试验的连接图如图所示。

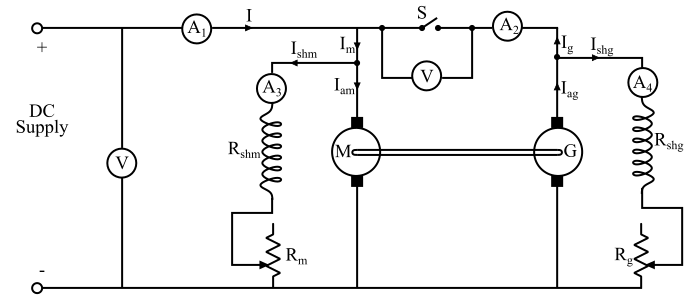
在连接图中，机器M作为电动机，并借助启动器从电源启动。开关S保持打开状态。机器M的励磁电流通过励磁调节器R_m进行调整，以使电动机以其额定速度运行。机器G作为发电机。

由于G由机器M驱动，因此它以M的额定速度运行。机器G的励磁电流通过其励磁调节器R_g进行调整，使得发电机G的电枢电压略高于电源电压。当发电机的电压等于母线电压且极性相同，则闭合开关S，将发电机连接到母线。

现在，两台机器并联连接到电源电压。在这种情况下，发电机既不从电源取电，也不向电源供电，因此被称为“浮动”。现在，通过使用励磁调节器调整机器的励磁，可以在机器上施加任何负载。

这里：

$$\mathrm{电源输入功率 = 𝑉𝐼}$$

来自电源的此输入功率等于两台机器的总损耗。

$$\mathrm{电动机电枢铜损 = I_{am}^{2}R_{a}}$$

$$\mathrm{电动机励磁铜损 = I_{shm}^{2}R_{shm}}$$

$$\mathrm{发电机电枢铜损 = I_{ag}^{2}R_{a}}$$

$$\mathrm{发电机励磁铜损 = I_{shg}^{2}R_{shg}}$$

由于两台机器相同，因此假设两台机器的恒定损耗Pc相等，其值为：

$$\mathrm{𝑃_{𝐶} = (电源输入功率) − (两台机器的电枢和并励铜损)}$$

$$\mathrm{⇒ 𝑃_{𝐶} = VI − (I_{am}^{2}R_{a}+I_{shm}^{2}R_{shm}+I_{ag}^{2}R_{a}+I_{shg}^{2}R_{shg})}$$

假设恒定损耗在两台机器之间平均分配。

$$\mathrm{\therefore 每一台机器的恒定损耗 =\frac{𝑃_{𝐶}}{2}}$$

现在，可以确定两台机器的效率如下：

发电机效率：

$$\mathrm{发电机输出 = 𝑉𝐼_{𝑎𝑔}}$$

$$\mathrm{发电机恒定损耗 =\frac{𝑃_{𝐶}}{2}}$$

$$\mathrm{发电机电枢铜损 = I_{ag}^{2}R_{a}}$$

$$\mathrm{发电机励磁铜损 = I_{shg}^{2}R_{shg}}$$

因此，发电机的效率由下式给出：

$$\mathrm{\eta_{𝑔} =\frac{输出}{输出 + 损耗} =\frac{𝑉𝐼_{𝑎𝑔}}{𝑉𝐼_{𝑎𝑔} + I_{ag}^{2}R_{a} + I_{shg}^{2}R_{shg} +\frac{𝑃_{𝐶}}{2}}}$$

电动机效率

$$\mathrm{电动机输入 = 𝑉𝐼_{𝑚} = 𝑉(𝐼_{𝑎𝑚} + 𝐼_{𝑠ℎ𝑚})}$$

$$\mathrm{电动机恒定损耗 =\frac{𝑃_{𝐶}}{2}}$$

$$\mathrm{电动机电枢铜损 = I_{am}^{2}R_{a}}$$

$$\mathrm{电动机励磁铜损 = I_{shm}^{2}R_{shm}}$$

因此，电动机的效率由下式给出：

$$\mathrm{\eta_{𝑚} =\frac{输入 − 损耗}{输入} =\frac{[𝑉(𝐼_{𝑎𝑚} + 𝐼_{𝑠ℎ𝑚})] − [I_{am}^{2}R_{a} + I_{shm}^{2}R_{shm} +\frac{𝑃_{𝐶}}{2}]}{𝑉(𝐼_{𝑎𝑚} + 𝐼_{𝑠ℎ𝑚})}}$$

霍普金森试验的优点

霍普金森试验测定直流电机效率的优点在于：

• 此方法非常经济，因为从电源汲取的功率非常低。
• 可以在额定负载条件下检查换向条件和温升。
• 可以确定不同负载下的效率。
• 可以测试大型直流电机，而不会浪费太多电力。
• 由于两台机器都在额定负载条件下运行，因此考虑了杂散损耗。

霍普金森试验的缺点

此测试的主要缺点是需要两台实际上相同的直流电机。因此，此测试仅适用于大型直流电机的制造商。

Saini Manish Kumar

更新于：2021年8月20日

8000+ 次查看

启动您的职业生涯

完成课程获得认证

开始学习