数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究什么是悬式绝缘子的串联效率？
串联效率
悬式绝缘子由多个瓷质圆盘通过金属连接件串联而成，形成一个串。
施加在悬式绝缘子串上的电压并非均匀地分布在各个圆盘上，即最靠近导线的圆盘的电位远高于其他圆盘。这种不均匀的电位分布是不希望出现的，通常用串联效率来表示。因此，悬式绝缘子的串联效率定义如下：
“整个串的电压与最靠近导线的圆盘的电压乘以串中圆盘数量的比值称为串联效率。”
$$\mathrm{\therefore 串联效率\mathrm{\, =\, }\frac{串电压}{最靠近导线圆盘电压\: \times \mathit{n}}}$$
其中，n 是悬式绝缘子串中圆盘的数量。
因此，从串联效率的定义可以看出，串联效率越高，电压在串上的分布越均匀。理想情况下，串联效率为 100%，每个圆盘上的电压完全相同。然而，要实现 100% 的串联效率是不可能的。
提高串联效率的方法
我们知道，悬式绝缘子串中的电位分布并不均匀，即最靠近导线的绝缘子圆盘上出现最高电位，并随着接近横臂而逐渐降低。
如果最靠近导线的圆盘绝缘击穿，其他圆盘也将依次发生击穿。因此，需要使串中各个圆盘上的电压均衡，即需要提高串联效率。
以下方法用于提高悬式绝缘子的串联效率：
使用较长的横臂
对绝缘子进行分级
使用保护环
使用较长的横臂
串联效率的值取决于并联电容与互电容的比率（设为 *K*）。也就是说，*K* 的值越小，串联效率越高，因此电位分布越均匀。
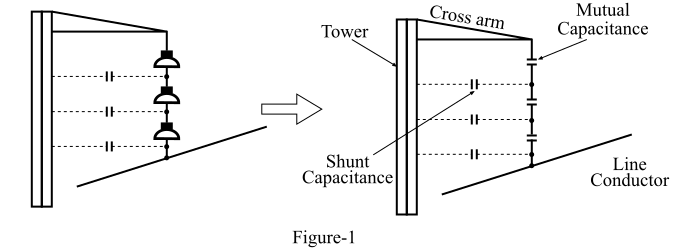
*K* 的值可以通过减小并联电容来降低。为了减少并联电容，必须增加导线与铁塔之间的距离，即使用较长的横臂。在实践中，*K* = 0.1 是此方法可以达到的极限。这是因为铁塔的成本和强度限制不允许使用非常长的横臂。
对绝缘子进行分级
在这种提高串联效率的方法中，选择不同尺寸的绝缘子，使每个绝缘子具有不同的电容。因此，使用的绝缘子是电容分级的，即以这样一种方式连接以形成串，使得顶部圆盘的电容最小，并随着接近最靠近导线的圆盘而逐渐增大。
由于电压与电容成反比，因此绝缘子的电容分级有助于使串中各个圆盘上的电位分布均衡。这种方法的主要缺点是需要大量不同尺寸的绝缘子。
使用保护环
保护环是一个金属环，它与导体电连接，并包围最下面的绝缘子圆盘，如图 2 所示。它使串中每个圆盘上的电位均衡。
保护环在金属配件和导线之间引入电容。保护环的设计使得并联电容电流 *𝑖1、𝑖2* 等等于金属配件线电容电流 *𝑖1′、𝑖2′* 等。结果是相同的充电电流（I）流过串中的每个圆盘。因此，串中圆盘上的电位分布将是均匀的。
数值示例
在 33 kV 架空输电线路上，绝缘子串中包含三个圆盘。如果最靠近导线的圆盘上的电压为 8 kV。然后，确定串联效率。
解决方案
$$\mathrm{串电压\mathrm{\, =\, }\frac{33}{\sqrt{3}}\mathrm{\, =\, }19.05 \: kV}$$
串联效率由下式给出：
$$\mathrm{串联效率\mathrm{\, =\, }\frac{串电压}{最靠近导线圆盘电压\: \times \mathit{n}}}$$
$$\mathrm{\therefore \% \: 串联效率\mathrm{\, =\, }\frac{19.05}{8\times 3}\times 100\mathrm{\, =\, }79.4\%}$$
14K+ 次查看
