戴维南定理和戴维南等效电路

戴维南定理用于确定任何一个电路元件上的电流或电压，而无需通过求解复杂的网络方程组。

戴维南定理的陈述

任何一个双端双向线性直流电路都可以用一个等效电路来代替，该等效电路由一个电压源串联一个电阻组成，电压源等于开路负载端子上的开路电压，电阻等于从开路负载端子看进去的电源网络的内阻。

戴维南定理的解释

步骤 1 – 去除负载电阻 (R_L) 并找到开路负载端子上的开路电压 (V_OC = V_Th)。

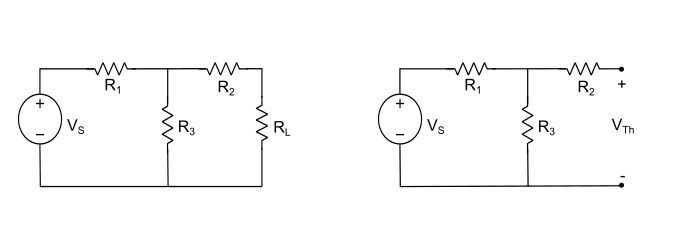
$$\mathrm{\mathit{V}_{rh}=\mathit{IR}_{3}=\mathit{V}_{s}\frac{\mathit{R}_{3}}{\mathit{R}_{1}+\mathit{R}_{3}}}$$

其中，I 是流过电阻 R₁ 和 R₃ 的闭环电流。

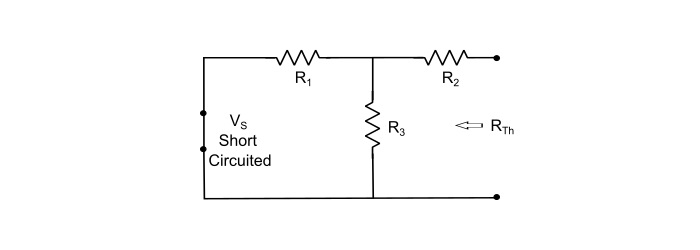
步骤 2  - 使恒定电源失效（对于电压源，通过其内阻去除，对于电流源，用开路代替电源）并找到从开路负载端子看进去的内阻 (R_Th)。

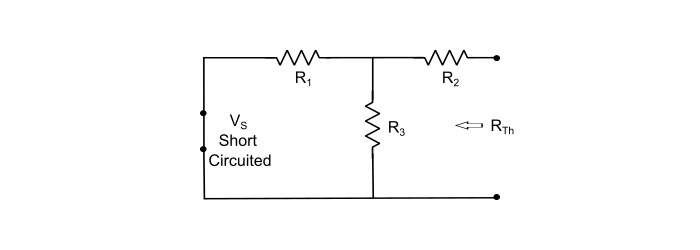
$$\mathrm{\mathit{R}_{Th}=\frac{\mathit{R}_{1}\mathit{R}_{3}}{\mathit{R}_{1}+\mathit{R}_{3}}+\mathit{R}_{2}}$$

步骤 3 获得戴维南等效电路，将 R_Th 与 V_Th 串联。将负载电阻 (R_L) 重新连接到负载端子上。然后，求出负载电流。

这里，负载电流 (I_L) 通过 RL 给出为：

$$\mathrm{\mathit{I}_{L}=\frac{\mathit{V}_{rh}}{\mathit{R}_{Th}+\mathit{R}_{L}}}$$

求戴维南等效电阻 (R_Th) 的方法

• 对于独立电源 – 包含独立电流源或电压源的任何线性双向网络的 R_Th 可以通过使用其内阻使电源失效来确定，即对于独立理想电压源，通过短路使其失效，对于独立理想电流源，通过去除电源使其失效。然后，找到从开路负载端子看进去的网络内阻。

• 对于包含从属电源或独立电源或两者兼而有之的电路

  • 第一种方法 求出开路负载端子上的 V_Th。接下来，短路负载端子并确定通过短路端子的短路电流 (I_SC)。内阻或戴维南等效电阻由下式给出：

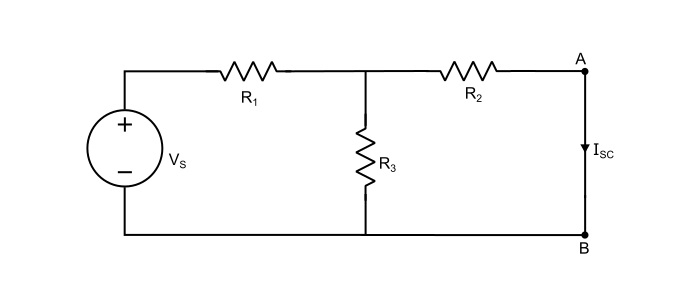
$$\mathrm{\mathit{R}_{Th}=\frac{\mathit{V}_{rh}}{\mathit{I}_{sc}}}$$

• 第二种方法 - 去除负载电阻并在开路负载端子上施加一个直流测试电压 (V_T)。在此期间，保持其他独立电源失效。由于施加了 V_T，直流电流 (I_T) 将从负载端子流入电路。源网络的内阻或戴维南等效电阻获得为：

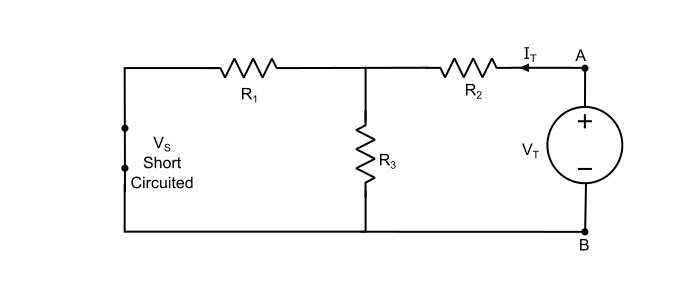
$$\mathrm{\mathit{R}_{Th}=\frac{\mathit{V}_{T}}{\mathit{I}_{T}}}$$

数值例子

使用戴维南定理，求下图中 10 Ω 电阻中的电流。已知电池内阻为 2 Ω。

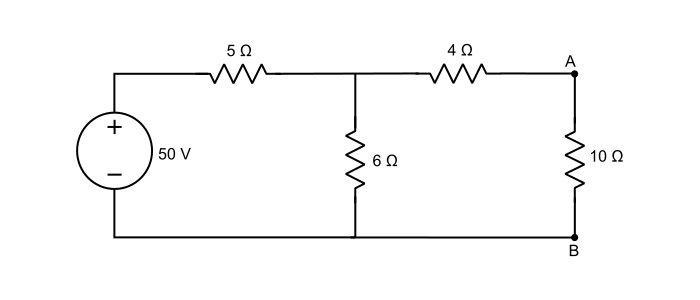
解决方案

步骤 1 – 去除负载电阻并确定负载端子上的开路电压 (V_Th)。

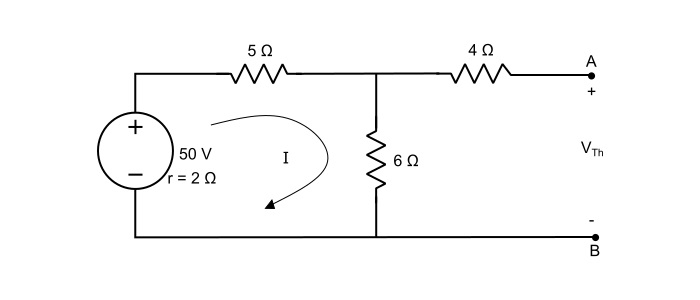
这里，当 10 Ω 电阻被移除时，在 4 Ω 上没有电压降，V_Th 将是出现在 6 Ω 电阻上的电压。因此，

$$\mathrm{\mathit{I}=\frac{50}{2+5+6}=\frac{50}{13}=3.846\:A}$$

当 10 Ω 电阻被移除时，在 4 Ω 电阻上没有电压降，V_Th 将是出现在 6 Ω 电阻上的电压。因此，

$$\mathrm{\mathit{V}_{Th}=\mathit{I}×6=3.846×6=23.076\:V}$$

步骤 2 – 要找到 R_Th，请使所有独立电源失效。如，

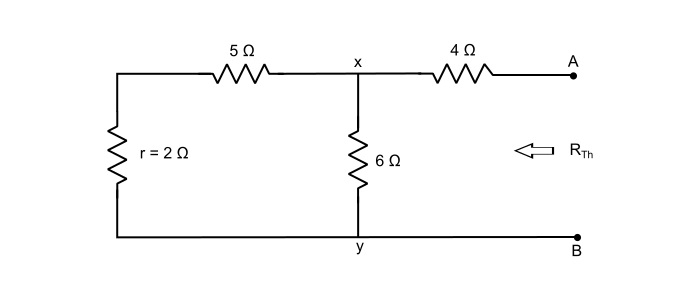
$$\mathrm{\mathit{R}_{xy}=(5+2)||6=\frac{7×6}{7+6}=3.23\:Ω}$$

$$\mathrm{\mathit{R}_{Th}=\mathit{R}_{xy}+4=3.23+4=7.23 \:Ω}$$

步骤 3 – 构造戴维南等效电路并将负载电阻重新连接以计算负载电流，如，

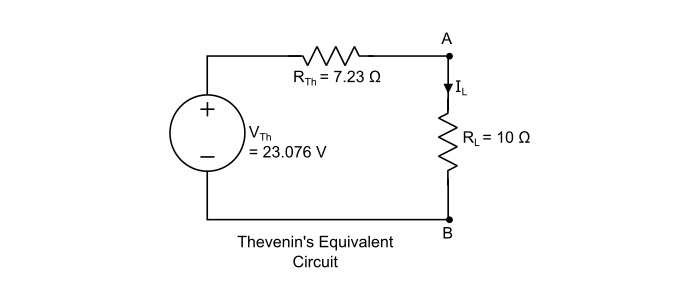
$$\mathrm{\mathit{I}_{L}=\frac{\mathit{V}_{rh}}{\mathit{R}_{rh}+\mathit{R}_{L}}=\frac{23.076}{7.23+10}=1.339\:A}$$

Manish Kumar Saini

更新于: 2021年6月18日

2K+ 浏览量

开启你的 职业生涯

通过完成课程获得认证

开始学习