双笼式感应电动机的等效电路

---

对于双笼式感应电动机，下标“s”和“r”分别表示定子和转子。

设：

• 𝑅_𝑠 = 每相定子电阻
• 𝑋_𝑠 = 每相定子电抗
• 𝑅′_𝑟𝑜 = 外笼每相转子电阻（折算到定子）
• 𝑋′_𝑟𝑜 = 外笼每相静止漏电抗（折算到定子）
• 𝑅′_𝑟𝑖 = 内笼每相转子电阻（折算到定子）
• 𝑋′_𝑟𝑖 = 内笼每相静止漏电抗（折算到定子）
• 𝑠 = 滑差率

如果认为主磁通完全穿过两个笼子，则可以认为两个笼子的阻抗是并联的。图1显示了滑差为s的双笼式感应电动机的等效电路。

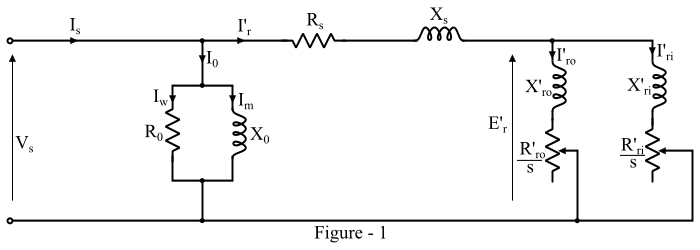
此处，转子阻抗由下式给出：

$$\mathrm{外笼阻抗,\: 𝑍′_{𝑟𝑜} =\frac{𝑅′_{𝑟0}}{𝑠}+ 𝑗𝑋′_{𝑟𝑜}}$$

$$\mathrm{内笼阻抗,\: 𝑍\:′_{𝑟𝑖} =\frac{𝑅′_{𝑟𝑖}}{𝑠}+ 𝑗𝑋′_{𝑟𝑖}}$$

并且，定子阻抗由下式给出：

$$\mathrm{定子阻抗, \:𝑍_𝑠 = 𝑅_𝑠 + 𝑗𝑋_𝑠}$$

在等效电路中，如果忽略包含R0和X0的并联支路，则可以得到双笼式感应电动机的近似等效电路，如下图所示。

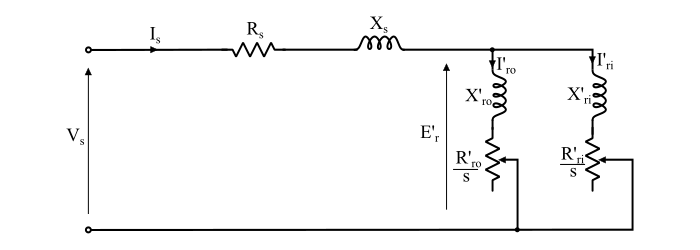
折算到定子的电动机每相等效阻抗由下式给出：

$$\mathrm{𝑍_{𝑒𝑠} = 𝑍_𝑠 + (𝑍′_{𝑟𝑜} || 𝑍′_{𝑟𝑖})}$$

$$\mathrm{⇒ 𝑍_{𝑒𝑠} = (𝑅_𝑠 + 𝑗𝑋_𝑠) + (\frac{𝑍′_{𝑟𝑜} 𝑍′_{𝑟𝑖}}{𝑍′_{𝑟𝑜}+ 𝑍′_{𝑟𝑖}})}$$

流过转子外笼的电流由下式给出：

$$\mathrm{𝐼′_{𝑟𝑜} =\frac{𝐸′_𝑟}{𝑍′_{𝑟𝑜}}}$$

流过转子内笼的电流由下式给出：

$$\mathrm{𝐼′_{𝑟𝑖} =\frac{𝐸′_𝑟}{𝑍′_{𝑟𝑖}}}$$

因此，折算到定子的转子电流等于外笼和内笼电流的相量和，即：

$$\mathrm{𝐼′_𝑟 = 𝐼′_{𝑟𝑜} + 𝐼′_{𝑟𝑖}}$$