感应电动机的等效电路、定子电路模型和转子电路模型

感应电动机的运行原理是基于定子电路在转子电路中感应电压和电流。感应电动机稳态条件下的性能特性可以通过其等效电路进行评估。由于三相感应电动机表示一个平衡负载，因此，其等效电路仅绘制一相。

感应电动机的定子电路模型

感应电动机的定子电路模型或定子等效电路如图所示。

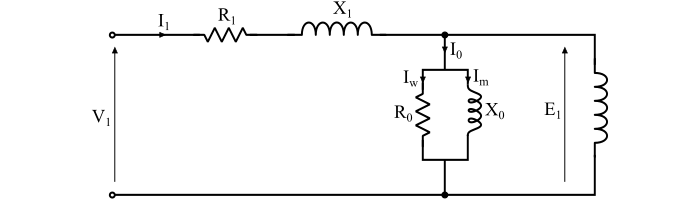
感应电动机的定子电路模型包括定子相绕组电阻R1、定子相绕组漏抗X₁。R₁和X₁直接出现在电机模型的输入端。纯感性电抗X₀表示感应电动机的励磁电抗，其值远大于其他电抗。非感性电阻R₀表示感应电动机的铁损分量。因此，感应电动机的空载电流I₀由励磁电抗（X₀）所产生的励磁电流（I_m）和铁损电阻（R0）所产生的铁损电流Iw的相量和给出。因此，

$$\mathrm{𝐼_0 = 𝐼_𝑚 + 𝐼_𝑤 … (1)}$$

由于感应电动机的空气隙导致较高的磁阻，因此感应电动机的空载电流（I₀）非常大（约为额定电流的25%到40%）。

感应电动机的转子电路模型

当三相电源电压施加到感应电动机的定子绕组时，会在感应电动机的转子绕组中感应出电压。实际上，转子和定子旋转磁场之间的相对运动越大，感应的转子电压就越大。

当转子静止时，相对运动最大。这种情况称为静止状态或锁转状态或堵转状态。

如果静止状态下的感应转子电压为E20，则任何滑差值下的感应转子电压由下式给出：

$$\mathrm{𝐸_2 = 𝑠𝐸_{20} … (2)}$$

转子电路的电阻（R₂）是恒定的，并且与感应电动机的滑差无关。

感应电动机的转子电路的电抗取决于转子绕组的电感和转子电流的频率。因此，如果L₂是转子的电感，则滑差s下的转子电抗由下式给出：

$$\mathrm{𝑋_2 = 2𝜋𝑓_2𝐿_2}$$

但转子频率为：

$$\mathrm{𝑓_2 = 𝑠𝑓_1}$$

$$\mathrm{\therefore\: 𝑋_2 = 2𝜋𝑠𝑓_1𝐿_2 = 𝑠(2𝜋𝑓_1𝐿_2) = 𝑠𝑋_{20} … (3)}$$

其中，X₂₀是静止转子电抗。

滑差s下转子的阻抗由下式给出：

$$\mathrm{𝑍_2 = 𝑅_2 + 𝑗𝑋_2 = 𝑅_2 + 𝑗𝑠𝑋_{20} … (4)}$$

因此，感应电动机的每相转子电流由下式给出：

$$\mathrm{𝐼_2 =\frac{𝐸_2}{𝑍_2}=\frac{𝑠𝐸_{20}}{𝑅_2 + 𝑗𝑠𝑋_{20}}… (5)}$$

使用此转子电流方程，可以绘制出感应电动机的转子电路模型，如图所示。

Manish Kumar Saini

更新于： 2021年8月25日

885 次浏览

开启您的职业生涯

通过完成课程获得认证

开始学习