并联电路：定义和示例

当电阻以一种方式连接，使得每个电阻的一端连接到一个公共点，而每个电阻的另一端连接到另一个公共点，电流流动的路径数等于电阻数时，这被称为并联电路。

解释

考虑三个电阻R₁、R₂和R₃连接到电压源V上，如图所示。总电流(I)分为三部分——I1流过R₁，I₂流过R₂，I₃流过R₃。可以看出，每个电阻上的电压相同。

根据欧姆定律，每个电阻的电流由下式给出：

$$\mathrm{\mathit{I}_{1}=\frac{\mathit{V}}{\mathit{R}_{1}};\:\:\:\mathit{I}_{2}=\frac{\mathit{V}}{\mathit{R}_{2}}\:\:\:and\:\:\:I_{3}=\frac{\mathit{V}}{\mathit{R}_{3}};}$$

参考电路图，总电流为：

$$\mathrm{\mathit{I}=\mathit{I}_{1}\:+\:\mathit{I}_{2}\:+\:\mathit{I}_{3}}$$

$$\mathrm{\Rightarrow\:\mathit{I}=\frac{\mathit{V}}{\mathit{R}_{1}}+\frac{\mathit{V}}{\mathit{R}_{2}}+\frac{\mathit{V}}{\mathit{R}_{3}}=\mathit{V}(\frac{1}{\mathit{R}_{1}}+\frac{1}{\mathit{R}_{2}}+\frac{1}{\mathit{R}_{3}})}$$

$$\mathrm{\Rightarrow\:\frac{\mathit{I}}{\mathit{V}}=(\frac{1}{\mathit{R}_{1}}+\frac{1}{\mathit{R}_{2}}+\frac{1}{\mathit{R}_{3}})}$$

$$\mathrm{∵\:\frac{\mathit{I}}{\mathit{V}}=\frac{1}{\mathit{R}_{p}}}$$

$$\mathrm{∵\:\frac{1}{\mathit{R}_{p}}=(\frac{1}{\mathit{R}_{1}}+\frac{1}{\mathit{R}_{2}}+\frac{1}{\mathit{R}_{3}})}$$

因此，当多个电阻并联连接时，总电阻的倒数等于各个电阻倒数的和。

此外，

$$\mathrm{∵\:\frac{1}{\mathit{R}}=\mathit{G}(电导)}$$

$$\mathrm{∵\:\mathit{G}_{p}=\mathit{G}_{1}+\mathit{G}_{2}+\mathit{G}_{3}}$$

因此，并联连接的电阻的总电导G_P等于其各个电导的和。

电路中总功耗等于各个电阻功耗的总和。因此，

$$\mathrm{\frac{1}{\mathit{R}_{p}}=(\frac{1}{\mathit{R}_{1}}+\frac{1}{\mathit{R}_{2}}+\frac{1}{\mathit{R}_{3}})}$$

$$\mathrm{\Rightarrow\frac{\mathit{V}^{2}}{\mathit{R}_{p}}=\frac{\mathit{V}^{2}}{\mathit{R}_{1}}+\frac{\mathit{V}^{2}}{\mathit{R}_{2}}+\frac{\mathit{V}^{2}}{\mathit{R}_{3}}}$$

$$\mathrm{\Rightarrow\:\mathit{P}_{p}=\mathit{P}_{1}+\mathit{P}_{2}+\mathit{P}_{3}}$$

并联电路的重要特征

• 每条支路上的电压相同。

• 随着并联支路数量的增加，电路的总电阻减小。

• 电路的总电阻小于最小的电阻值。

• 总电导等于各个电导的和。

• 电路的总功耗等于各个电阻功耗的和。

数值示例

如图所示电路中，A点和B点之间的电位差是多少？求出三条支路的电流。

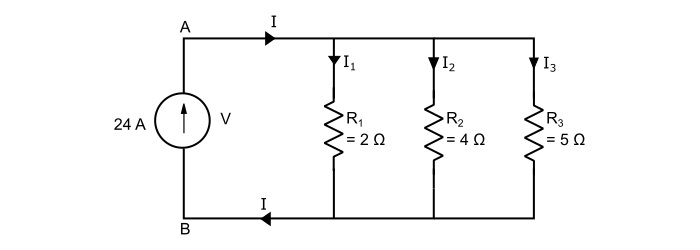
解答

三个并联电阻的等效电阻(R_P)为

$$\mathrm{\frac{1}{\mathit{R}_{p}}=\frac{1}{2}+\frac{1}{4}+\frac{1}{5}=\frac{19}{20}}$$

$$\mathrm{\Rightarrow\:{\mathit{R}_{p}}=1.053 \:Ω}$$

因此，A点和B点之间的电压V为

$$\mathrm{\mathit{V}=I\mathit{R}_{p}=24×1.053=25.27\:伏特}$$

现在，支路电流为

$$\mathrm{电流\:\mathit{I}_{1}=\frac{\mathit{V}}{\mathit{R}_{1}}=\frac{25.27}{2}=12.64\:安培}$$

$$\mathrm{电流\:\mathit{I}_{2}=\frac{\mathit{V}}{\mathit{R}_{2}}=\frac{25.27}{4}=6.32\:安培}$$

$$\mathrm{电流\:\mathit{I}_{3}=\frac{\mathit{V}}{\mathit{R}_{3}}=\frac{25.27}{5}=5.05\:安培}$$

Saini Manish Kumar

更新于：2021年6月18日

浏览量：1000+

开启你的职业生涯

完成课程获得认证

开始学习