分布系数或宽度系数 – 定义、公式和示例

在集中绕组中，给定相位的线圈边集中在一个给定磁极下的单个槽中。各个线圈中的感应电动势彼此同相。因此，这些电动势可以算术相加。为了确定集中绕组中每相的感应电动势，将给定的线圈电动势乘以每相串联连接的线圈数。

在实际应用中，交流发电机每相绕组的线圈并非集中在一个槽中，而是分布在多个槽中，以在每个磁极下形成一个极组。构成极组的线圈边中感应的电动势并非同相，而是相差一个角，该角等于槽的角位移 (β)。任何相位中产生的总电压将是各个线圈电压的相量和。

**分布系数**或**宽度系数**定义为分布绕组感应电动势与集中绕组感应电动势之比，即

$$\mathrm{分布系数, 𝑘_{𝑑} =\frac{分布绕组电动势}{集中绕组电动势}… (1)}$$

设：

$$\mathrm{𝑚 = 每极每相槽数 =\frac{槽数}{磁极数 \times 相数}}$$

$$\mathrm{β = 相邻槽之间的电角度位移}$$

$$\mathrm{β =\frac{180° \times 磁极数}{槽数}}$$

因此，绕组的一个相位由排列在 m 个连续槽中的线圈组成。𝐸_𝐶1、𝐸_𝐶2、𝐸_𝐶3……是各个线圈电动势。每个线圈电动势 𝐸_𝐶 将与下一个线圈电动势相差槽距 (β)。

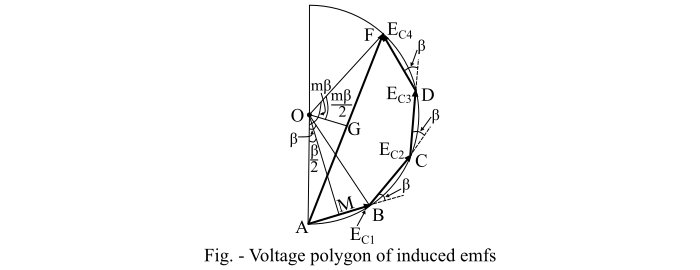
参考图中所示的一组四个线圈中感应电动势的电压多边形。这里，电动势 𝐸_𝐶1、𝐸_𝐶2、𝐸_𝐶3 和 𝐸_𝐶4 分别由相量 AB、BC、CD 和 DF 表示。这些相量中的每一个都是以 O 为中心的圆的弦，并在中心 O 处张成一个角度 β。相量 AF 代表给出合绕组电压的相量和，并在 O 处张成一个角度 mβ。

现在，分布系数也可以表示为

$$\mathrm{𝑘_{𝑑} =\frac{每相线圈电压的相量和}{每相线圈电压的算术和}… (2)}$$

各个线圈电压的算术和由下式给出：

$$\mathrm{线圈电压算术和 = 𝑚𝐸_{𝐶} = 𝑚 ∙ 𝐴𝐵 = 𝑚 ∙ (2𝐴𝑀)}$$

$$\mathrm{\Rightarrow\:线圈电压算术和 = 2𝑚 ∙ 𝑂𝐴\:sin \angle 𝐴𝑂𝑀}$$

$$\mathrm{= 2𝑚 ∙ 𝑂𝐴\:sin(β/2)}$$

各个线圈电压的相量和由下式给出：

$$\mathrm{线圈电压相量和 = 𝐴𝐹 = 2𝐴𝐺 = 2 ∙ 𝑂𝐴\:sin \angle 𝐴𝑂𝐺}$$

$$\mathrm{= 2 ∙ 𝑂𝐴\:sin(𝑚 β/2)}$$

因此，分布系数可以写成：

$$\mathrm{𝑘_{𝑑} =\frac{每相线圈电压相量和}{每相线圈电压算术和}=\frac{2 ∙ 𝑂𝐴 sin(𝑚 β/2)}{2𝑚 ∙ 𝑂𝐴\:sin(β/2)}}$$

$$\mathrm{\Rightarrow\:𝑘_{𝑑} =\frac{sin(𝑚 β/2)}{m\:sin(β/2)}… (3)}$$

从公式 (3) 可以看出，对于给定的相数，分布系数仅取决于给定磁极下分布槽的数量。它与绕组类型、每线圈匝数等无关。随着每极槽数的增加，分布系数减小。

数值示例

一台三相、50 Hz、6 极交流发电机具有星形连接绕组，有 180 个槽，每个槽有 10 根导线。假设线圈是满极距线圈。确定绕组分布系数。

解答

每极每相槽数由下式给出：

$$\mathrm{𝑚 =\frac{槽数}{磁极数 \times 相数}=\frac{180}{6 \times 3}= 10}$$

槽距为：

$$\mathrm{β =\frac{180° \times 磁极数}{槽数}=\frac{180° \times 6}{180}= 6°}$$

因此，绕组分布系数由下式给出：

$$\mathrm{𝑘_{𝑑} =\frac{sin(𝑚 β/2)}{m\:sin(β/2)}=\frac{sin(\frac{10 × 6}{2})}{10 × sin(\frac{6°}{2})}=\frac{0.5}{0.523}= 0.956}$$

Saini Manish Kumar

更新于：2021年9月30日

5K+ 次浏览

开启你的职业生涯

完成课程获得认证

开始学习