同步发电机中的节距因数或线圈跨距因数

线圈跨距或线圈节距定义为线圈两侧之间的距离。

极距定义为一个磁极中心线到下一个磁极中心线的角度距离。无论机器上有多少个磁极，极距始终为 180° 电气角。

• 当线圈跨距为 180° 电气角时，称为全节距线圈。

• 当线圈跨距小于 180° 电气角时，称为短节距线圈或分段节距线圈。

分段节距线圈也称为弦线圈。使用分段节距线圈的定子绕组称为弦绕组。

如果线圈跨距减少了 α 电气角，则线圈跨距将为 (180 − α) 电气度。

对于全节距线圈，两个线圈边跨越的距离正好等于 180° 电气角的极距。因此，全节距线圈中产生的电压使得线圈边电压同相。

设 $𝐸_{𝐶1}$ 和 $𝐸_{𝐶2}$ 是线圈两边产生的电压，$𝐸_{𝐶}$ 是线圈的合成电压。然后，

$$\mathrm{𝑬_{𝑪} = 𝑬_{𝑪𝟏} + 𝑬_{𝑪𝟐}}$$

由于 $𝐸_{𝐶1}$ 和 $𝐸_{𝐶2}$ 同相，因此合成线圈电压等于它们的算术和（参考全节距线圈图）。

$$\mathrm{∴\:𝐸_{𝐶} = 𝐸_{𝐶1} + 𝐸_{𝐶2}}$$

如果单个线圈的线圈跨距小于 180° 电气角的极距，即短节距线圈的情况，则每个线圈边产生的电压不同相。合成线圈电压 $𝐸_{𝐶}$ 等于 $𝐸_{𝐶1}$ 和 $𝐸_{𝐶2}$ 的相量和。

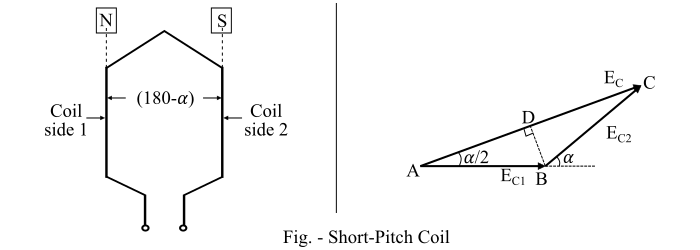
如果线圈跨距减少了 α 电气角，则线圈跨距为 (180 − α) 电气度。两个线圈边产生的电压 $𝐸_{𝐶1}$ 和 $𝐸_{𝐶2}$ 相互之间将相差 α° 电气角。$𝐸_{𝐶1}$ 和 $𝐸_{𝐶2}$ 的相量和为 $𝐸_{𝐶}$ = 𝐴𝐶（参考短节距线圈图）。

线圈跨距因数或节距因数定义为短节距线圈中产生的电压与全节距线圈中产生的电压之比。线圈跨距因数也称为弦距因数。

$$\mathrm{线圈跨距因数, 𝑘_{𝐶} =\frac{短节距线圈产生的电压}{全节距线圈产生的电压}}$$

参考相量图，

$$\mathrm{𝑘_{𝐶} =\frac{两个线圈边电压的相量和}{两个线圈边电压的算术和}=\frac{𝐴𝐶}{2𝐴𝐵}}$$

$$\mathrm{\Rightarrow\:𝑘_{𝐶} =\frac{2𝐴𝐷}{2𝐴𝐵}= cos\left(\frac{α}{2}\right)}$$

对于全节距线圈，

$$\mathrm{α = 0°;\:\:\:cos\frac{α}{2}= 1;\:\:\:or\:\:\: 𝑘_{𝐶} = 1}$$

对于短节距线圈，

$$\mathrm{𝑘_{𝐶} < 1}$$

弦绕法的优点

弦绕法的优点如下：

• 由于弦绕缩短了绕组的端部，因此可以节省导体材料。

• 弦绕或短节距可以减少失真谐波的影响，从而改善产生的电压波形，使其更接近正弦波。

Manish Kumar Saini

更新于: 2021-10-01

12K+ 次查看

开启你的 职业生涯

通过完成课程获得认证

开始学习